Bài 1 trang 121 - SGK Giải tích 12

Tính diện tích hình phẳng giới hạn bởi các đường:

a) \(y={x^2},y =x + 2\);   

b) \(y = |lnx|, y = 1\);

c) \(y = {\left( x-6 \right)}^2,y = 6x-{x^2}\)

Giải

a) Phương trình hoành độ giao điểm \(f(x) = x^2-x -2 =0 ⇔ x = -1\) hoặc \(x = 2\).

Diện tích hình phẳng cần tìm là :

\(S=\int_{-1}^{2}\left |x^{2}- x- 2 \right |dx = \left | \int_{-1}^{2}\left (x^{2}- x- 2 \right ) dx \right |\)

    \(=\left |\frac{x^{3}}{3}-\frac{x^{2}}{2}-2x|_{-1}^{2} \right |=\left |\frac{8}{3}-2-4-(\frac{1}{3}-\frac{1}{2}+2) \right |\)\(=4\tfrac{1}{2}\)

b) Phương trình hoành độ giao điểm: 

\(f(x) = 1 - ln|x| = 0  ⇔ lnx = ± 1\)

\(⇔ x = e\) hoặc \(x = \frac{1}{e}\)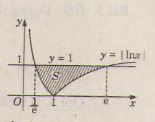                                                    

        \(y = ln|x| = lnx\) nếu \(lnx ≥ 0\) tức là \(x ≥ 1\).

 hoặc  \(y = ln|x| = - lnx\) nếu \(lnx < 0\), tức là \(0 < x < 1\).

Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :  

\(S=\int_{\frac{1}{e}}^{e}|1- ln|x||dx =\int_{\frac{1}{e}}^{1}(1+lnx)dx \)

\(+\int_{1}^{e}(1-lnx)dx\)

     \(= x|_{\frac{1}{e}}^{1}+\int_{\frac{1}{e}}^{1}lnxdx +x|_{1}^{e}-\int_{1}^{e}lnxdx\)

     \(=-\frac{1}{e}+e+\int_{\frac{1}{e}}^{1}lndx-\int_{1}^{e}lnxdx\)

Ta có  \(∫lnxdx = xlnx - ∫dx = xlnx  –  x  + C\),  thay vào trên ta được  :

\(S=e-\frac{1}{e}+(xlnx-x)|_{\frac{1}{e}}^{1}- (xlnx-x)|_{1}^{e}\)\(=e+\frac{1}{e}-2\)

c) Phương trình hoành độ giao điểm là:

\(f\left( x \right) =6x-{x^2}-{\left( {x -6} \right)^2} = - 2({x^2}-9x+ 18)\)\(=0\)

\(⇔  - 2({x^2}-9x+ 18) ⇔ x = 3\) hoặc \(x = 6\).

Diện tích cần tìm là:

\(S=\int_{3}^{6}|-2(x^{2}-9x+18)|dx\)

\(=|2\int_{3}^{6}(x^{2}-9x+18)dx|\)

\(=\left |2(\frac{x^{3}}{3}-\frac{9}{2}x^{2}+18x)|_{3}^{6} \right |=9\).

Bài 2 trang 121 - SGK Giải tích 12

Tính diện tích hình phẳng giới hạn bởi đường cong \(y = {x^2} + 1\), tiếp tuyến với đường thẳng này

tại điểm \(M(2;5)\) và trục \(Oy\).

Giải

Phương trình tiếp tuyến là \(y = 4x - 3\).

Phương trình hoành độ giao điểm

 \({x^2} + 1 =4x - 3 \Leftrightarrow {x^2} - 4x + 4= 0 ⇔ x = 2\).

Do đó diện tích phải tìm là:

\(S=\int_{0}^{2}|x^{2}+1 -4x+3|dx=\int_{0}^{2}(x^{2}-4x+4)dx\)

\(=\frac{8}{3}=2\tfrac{2}{3}\).

Bài 3 trang 121 - SGK Giải tích 12

Parabol \(y = {{{x^2}} \over 2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt2\) thành hai phần. Tìm tỉ số diện tích của chúng.

Giải

Đường tròn đã cho có phương trình \({x^{2}} + {\rm{ }}{y^2} = {\rm{ }}8\)

Từ đó ta có: \(y =  \pm \sqrt {8 + {x^2}} \)

Tọa độ giao điểm của \((C)\) và \((P)\) thỏa mãn hệ: 

\(\left\{ \matrix{
{x^2} = 2y \hfill \cr 
{x^2} + {y^2} = 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{y^2} + 2y - 8 = 0 \hfill \cr 
{x^2} = 2y \hfill \cr} \right.\)

\( \Leftrightarrow \left\{ \matrix{
y = 2 \hfill \cr 
x = \pm 2 \hfill \cr} \right.\)

\(S_1 = 2\int_0^2 {\left( {\sqrt {8 - {x^2}}  - {{{x^2}} \over 2}} \right)} d{\rm{x}}\)

\(= 2\int\limits_0^2 {\sqrt {8 - {x^2}} dx - \left[ {{{{x^3}} \over 3}} \right]} \left| {_0^2 = 2\int\limits_0^2 {\sqrt {8 - {x^2}} } dx - {8 \over 3}} \right.\)

Đặt \(x = 2\sqrt 2 \sin t \Rightarrow dx = 2\sqrt 2 {\mathop{\rm costdt}\nolimits} \)

Đổi cận: \(\eqalign{
& x = 0 \Rightarrow t = 0 \cr 
& x = 2 \Rightarrow t = {\pi \over 4} \cr} \)

\({S_1} = 2\int\limits_0^{{\pi  \over 4}} {\sqrt {8 - 8{{\sin }^2}t} .2\sqrt 2 {\rm{costdt - }}{8 \over 3}} \)

\( = 16\int\limits_0^{{\pi  \over 4}} {{{\cos }^2}tdt - {8 \over 3}} \)\( = 8\int\limits_0^{{\pi  \over 4}} {(1 + cos2t)dt - {8 \over 3}} \)

\(= [8t + 4sint2t]|_0^{{\pi  \over 4}} - {8 \over 3} = 2\pi  + {4 \over 3}\)

Diện tích hình tròn là: \(\pi R^2=8\pi\)

và  \({S_2} = 8\pi  - {S_1}=6\pi+{4\over 3}.\)

Vậy  \({{{S_2}} \over {{S_1}}} = {{9\pi  - 2} \over {3\pi  + 2}}\).

Giaibaitap.me