Bài 1 trang 145 SGK Giải tích 12

Cho hàm số:

$f(x) = ax^2– 2(a + 1)x + a + 2 ( a ≠ 0)$

a) Chứng tỏ rằng phương trình f(x)  = 0 luôn có nghiệm thực. Tính các nghiệm đó.

b) Tính tổng $S$ và tích $P$ của các nghiệm của phương trình $f(x) = 0$. Khảo sát sự biến thiên và vẽ đồ thị hàm số của $S$ và $P$ theo $a$.

Giải

Ta có:

$f(x) = ax^2– 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2)$ nên phương trình $f(x) = 0$ luôn có hai nghiệm thực là:

$x = 1, x = {{a + 2} \over a}$

Theo định lí Vi-et, tổng và tích của các nghiệm đó là:

 $S = {{2a + 2} \over a},P = {{a + 2} \over a}$

1. Khảo sát sự biến thiên và vẽ đồ thị hàm số $S = {{2a + 2} \over a} = 2 + {2 \over a}$

- Tập xác định : $(-∞, 0)∪ (0, +∞)$

- Sự biến thiên: $S' =  - {2 \over {{a^2}}} < 0,\forall a \in ( - \infty ,0) \cup (0, + \infty )$ nên hàm số nghịch biến trên hai khoảng $(-∞, 0)$ và $(0, +∞)$

- Cực trị: Hàm số không có cực trị

- Giới hạn tại vô cực và tiệm cận ngang

$\eqalign{ & \mathop {\lim }\limits_{a \to + \infty } S = \mathop {\lim }\limits_{a \to + \infty } (2 + {2 \over a}) = 2 \cr  & \mathop {\lim }\limits_{a \to - \infty } S = \mathop {\lim }\limits_{a \to - \infty } (2 + {2 \over a}) = 2 \cr}$

Vậy $S = 2$ là tiệm cận ngang

- Giới hạn vô cực và tiệm cận đứng:

$\eqalign{ & \mathop {\lim }\limits_{a \to {0^ + }} S = \mathop {\lim }\limits_{a \to {0^ + }} (2 + {2 \over a}) = + \infty \cr  & \mathop {\lim }\limits_{a \to {0^ - }} S = \mathop {\lim }\limits_{a \to {0^ - }} (2 + {2 \over a}) = - \infty \cr}$

Vậy $a = 0$ là tiệm cận đứng.

- Bảng biến thiên:

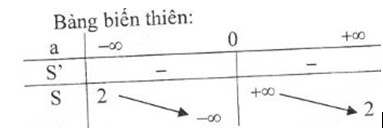
Đồ thị hàm số:

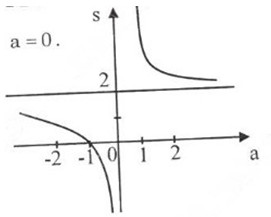
Đồ thị không cắt trục tung, cắt trục hoành tại $a = -1$

2) Khảo sát sự biến thiên và vẽ đồ thị hàm số $P = {{a + 2} \over a} = 1 + {2 \over a}$

Tập xác định: $D = \mathbb R\backslash {\rm{\{ }}0\}$

 $S' = {{ - 2} \over {{a^2}}} < 0,\forall a \in D$

$\mathop {\lim }\limits_{a \to {0^ - }} S =  - \infty  ⇒$Tiệm cận đứng: $a = 0$

$\mathop {\lim }\limits_{a \to  \pm \infty } S = 1⇒$ Tiệm cận ngang: $S = 1$

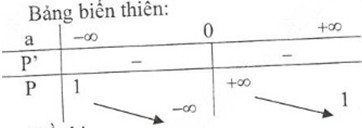
Đồ thị hàm số:

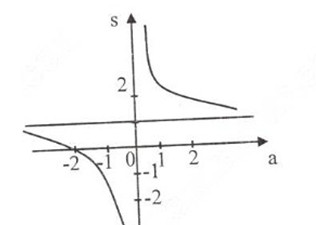
Ngoài ra: đồ thị hàm số $P = {{a + 2} \over a} = 1 + {2 \over a}$ có thể nhận được bằng cách tịnh tiến đồ thị $S = {{2a + 2} \over a} = 2 + {2 \over a}$ dọc theo trục tung xuống phía dưới $1$ đơn vị.

Bài 2 trang 145 SGK Giải tích 12

Cho hàm số: $y =  - {1 \over 3}{x^3} + (a - 1){x^2} + (a + 3)x - 4$

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số khi $a = 0$

b) Tính diện tích hình phẳng giới hạn bởi (C) và đường thẳng $y = 0, x = -1, x = 1$

Giải

a) Khi $a = 0$ ta có hàm số: $y =  - {1 \over 3}{x^3} - {x^2} + 3x - 4$

- Tập xác định : $(-∞, +∞)$

- Sự biến thiên: $y’= -x^2 – 2x + 3$

$y’=0 ⇔ x = 1, x = -3$

Trên các khoảng $(-∞, -3)$ và $(1, +∞), y’ < 0$ nên hàm số nghịch biến.

Trên khoảng $(-3, 1), y’ > 0$

_ Cực trị:

Hàm số đạt cực đại tại $x = 1$, ${y_{CD}} = {{ - 7} \over 3}$

Hàm số đạt cực tiểu tại $x = -3$, ${y_{CT}} =  - 13$

_ giới hạn vô cực : $\mathop {\lim }\limits_{x \to  + \infty }  =  - \infty ,\mathop {\lim }\limits_{x \to  - \infty }  =  + \infty$

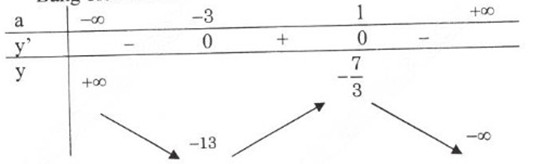
Bảng biến thiên:

Đồ thị hàm số:

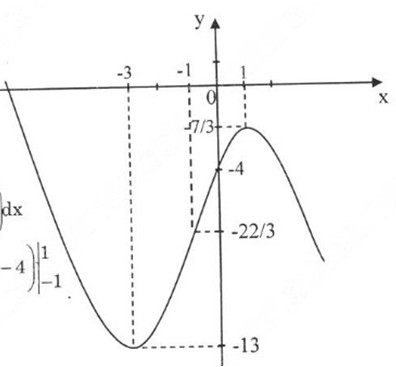
Đồ thị cắt trục tung tại $y = -4$

Đồ thị cắt trục hoành tại $x ≈ 5, 18$

b) Hàm số $y =  - {1 \over 3}{x^3} - {x^2} + 3x - 4$ đồng biến trên khoảng $(-3, 1)$ nên:

$y < y(1) = {{ - 7} \over 3} < 0$,  $∀x ∈ (-1, 1)$

Do đó , diện tích cần tính là:

$\int_{ - 1}^1 {( - {1 \over 3}{x^3} - {x^2} + 3x - 4} )dx = {{26} \over 3}$

Bài 3 trang 146 SGK Giải tích 12

Cho hàm số : y = x³ + ax² + bx + 1

a) Tìm a và b để đồ thị của hàm số đi qua hai điểm A(1, 2) và B(-2, -1)

b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị  tìm được của a và b.

c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường thẳng y = 0, x = 0, x = 1 và đồ thị (C) quanh trục hoành.

Giải

a) Đồ thị hàm số đi qua hai điểm A(1, 2) và B (-2, -1) khi và chỉ khi: 

$\left\{ \matrix{ 2 = 1 + a + b + 1 \hfill \cr  - 1 = - 8 + 4a - 2b + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = 1 \hfill \cr  b = - 1 \hfill \cr} \right.$

b) Khi a = 1, b = -1 ta có hàm số: y = x³ + x² – x + 1

_ Tập xác định: (-∞, + ∞)

_ Sự biến thiên: y’ = 3x² + 2x – 1

y’= 0 ⇔ x = -1, x = ${1 \over 3}$

Trên các khoảng (-∞, -1) và $({1 \over 3}, + \infty )$ , y’>0 nên hàm số đồng biến

Trên khoảng $( - 1,{1 \over 3})$  , y’ < 0 nên hàm số nghịch biến

_ Cực trị: Hàm số đạt cực đại tại x = -1, y_CD = 2

Hàm số đạt cực tiểu tại $x = {1 \over 3},{y_{CT}} = {{22} \over {27}}$

_ Giới hạn tại vô cực: $\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty ;\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty$

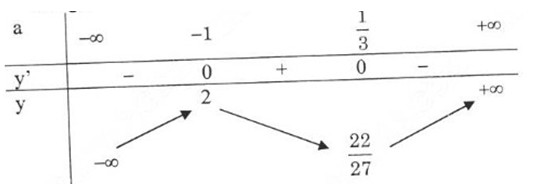
Bảng biến thiên:

Đồ thị hàm số:

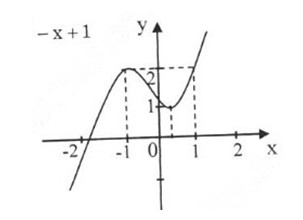
Đồ thị cắt trục tung tại y = 1, cắt trục hoành tại x ≈ -1, 84

c) Trong khoảng (0, 1) ta có y > 0.

Vì vậy, thể tích cần tìm là:

$V = \pi \int_0^1 {({x^3}}  + {x^2} - x + 1{)^2}dx = {{134\pi } \over {105}}$

Bài 4 trang 146 SGK Giải tích 12

Xét chuyển động thẳng xác định bởi phương trình:

 $s(t) = {1 \over 4}{t^4} - {t^3} + {{{t^2}} \over 2} - 3t$

Trong đó t được tính bằng giây và s được tính bằng $m$.

a) Tính $v(2), a(2)$, biết $v(t), a(t)$ lần lượt là vận tốc, gia tốc của chuyển động đã cho

b) Tính thời điểm $t$ mà tại đó vận tốc bằng $0$.

Giải

a) Ta có:

$v(t) = s’(t) = {t^{3}} - 3{t^2} + t - 3$

$a(t) = s’’(t) = 3t^2 – 6t + 1$

Do đó: $v(2) = -5; a(2) = 1$

b) $v(t) = 0 ⇔ t^3– 3t^2 + t – 3$

$⇔ t = 3$

Vậy tại thời điểm $t  = 3$ thì vận tốc bằng $0$.

Giaibaitap.me