Bài 71 trang 32 sgk toán 8 tập 1

Không thực hiện phép chia, hãy xét xem đa thức \(A\) có chia hết cho đa thức \(B\) hay không.

a) \(A = 15{x^4} - 8{x^3} + {x^2}\)

    \(B = {1 \over 2}{x^2}\)

b) \(A = {x^2} - 2x + 1\)

    \(B = 1 - x\)

Bài giải:

a) \(A,B\) là các đa thức một biến. \(A\) chia \(B\) thì ta lấy từng hạng tử của đa thức \(A\) chia cho  đa thức \(B\).

\({x^4},{x^3},{x^2}\) đều chia hết cho \(x^2\)

Do đó \(A\) chia hết cho \(B\)

b) \(A = {x^2} - 2x + 1={(1 - x)^2}\)

Do đó \(A\) chia hết cho \(B\).

Bài 72 trang 32 sgk toán 8 tập 1

 Làm tính chia:

\((2{x^4} + {\rm{ }}{x^3}-{\rm{ }}3{x^2} + {\rm{ }}5x{\rm{ }}-{\rm{ }}2){\rm{ }}:{\rm{ }}({x^2}-{\rm{ }}x{\rm{ }} + {\rm{ }}1)\)

Bài giải:

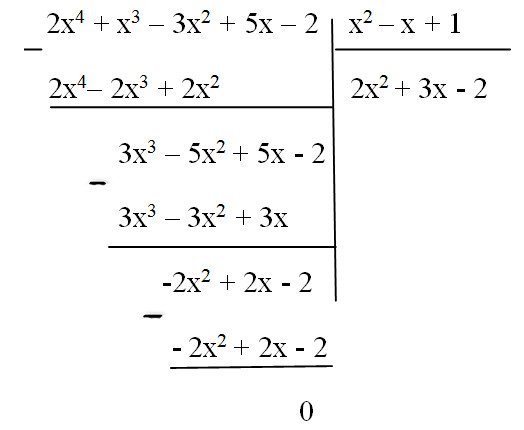
Bài 73 trang 32 sgk toán 8 tập 1

 Tính nhanh:

a) \((4{x^2}-{\rm{ }}9{y^2}){\rm{ }}:{\rm{ }}\left( {2x{\rm{ }}-{\rm{ }}3y} \right)\);                    

b) \((27{x^3}-{\rm{ }}1){\rm{ }}:{\rm{ }}\left( {3x{\rm{ }}-{\rm{ }}1} \right)\);

c) \((8{x^3} + {\rm{ }}1){\rm{ }}:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1)\);                

d) \(({x^2}-{\rm{ }}3x{\rm{ }} + {\rm{ }}xy{\rm{ }} - 3y){\rm{ }}:{\rm{ }}\left( {x{\rm{ }} + {\rm{ }}y} \right)\)

Bài giải:

a) \((4{x^2}-{\rm{ }}9{y^2}){\rm{ }}:{\rm{ }}\left( {2x{\rm{ }}-{\rm{ }}3y} \right) \)

\(= \left[ {{{(2x)}^2} - {{(3y)}^2}} \right]:(2x - 3y)\)

\(= (2x - 3y).(2x + 3y):(2x - 3y) = 2x + 3y\);        

b) \((27{x^3}-{\rm{ }}1){\rm{ }}:{\rm{ }}\left( {3x{\rm{ }}-{\rm{ }}1} \right) =\left[ {{{(3x)}^3} - {1^3}} \right]:(3x - 1)\)

\(= (3x - 1).\left[ {{{(3x)}^2} + 3x + 1} \right]:(3x - 1) \)

\(= 9{x^2} + 3x + 1\)

c) \((8{x^3} + {\rm{ }}1){\rm{ }}:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1){\rm{ }}\)

\(= \left[ {{{(2x)}^3} + {1^3}} \right]:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1)\)

\(= {\rm{ }}\left( {2x{\rm{ }} + {\rm{ }}1} \right)\left[ {{{(2x)}^2} - 2x + 1} \right]{\rm{ }}:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1)\)

\( = \left( {2x{\rm{ }} + {\rm{ }}1} \right)(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1):(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1){\rm{ }}\)

\(= {\rm{ }}2x{\rm{ }} + {\rm{ }}1\)                  

d) \(({x^2}-{\rm{ }}3x{\rm{ }} + {\rm{ }}xy{\rm{ }} - 3y){\rm{ }}:{\rm{ }}\left( {x{\rm{ }} + {\rm{ }}y} \right)\)

\(\eqalign{
& = \left[ {({x^2} + xy) - (3x + 3y)} \right]:(x + y) \cr
& = \left[ {x(x + y) - 3(x + y)} \right]:(x + y) \cr
& = (x + y)(x - 3):(x + y) \cr
& = x - 3 \cr
& \cr} \)

Bài 74 trang 32 sgk toán 8 tập 1

Tìm số \(a\) để đa thức \(2{x^3} - 3{x^2} + x + a\) chia hết cho đa thức \(x + 2\)

Bài giải:

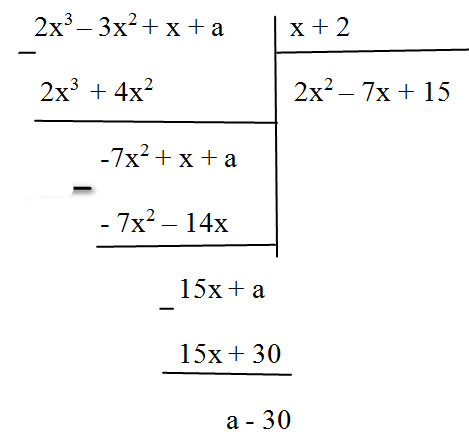
Ta có: \(2{x^3} - 3{x^2} + x + a \)

\(= (2{x^2} - 7x + 15).(x + 2) + a - 30\)

Dư trong phép chia là \((a-30)\) để phép chia là phép chia hết thì dư của phép chia phải bằng \(0\) tức là:

\(a-30=0\Rightarrow a=30\)

Vậy \(a = 30\).

Giaibaitap.me