Bài 80 trang 33 sgk toán 8 tập 1

Làm tính chia:

a) \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)            

b) \(\left( {{x^4} - {x^3} + {x^2} + 3x} \right):\left( {{x^2} - 2x + 3} \right)\) ;

c) \(\left( {{x^2} - {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\) .

Hướng dẫn làm bài:

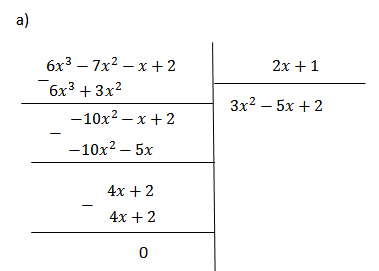
b)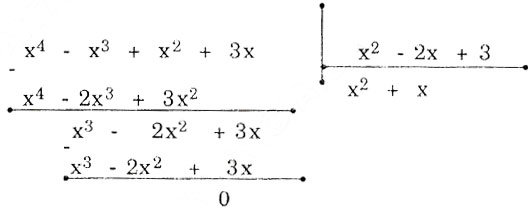 

c) \(\left( {{x^2} - {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\)

=\(\left( {{x^2} + 6x + 9 - {y^2}} \right)\left( {x + y + 3} \right)\)

=\(\left[ {\left( {{x^2} + 2x.3 + {3^2}} \right) - {y^2}} \right]:\left( {x + y + 3} \right)\)

=\(\left[ {{{\left( {x + 3} \right)}^2} - {y^2}} \right]:\left( {x + y + 3} \right)\)

=\(\left( {x + 3 - y} \right)\left( {x + 3 + y} \right):\left( {x + y + 3} \right)\)

= \(x + 3 - y\)

= \(x - y + 3\)

Bài 81 trang 33 sgk toán 8 tập 1

Tìm \(x\), biết:

a) \({2 \over 3}x\left( {{x^2} - 4} \right) = 0\) ;                                     

b) \({\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\) ;

c) \(x + 2\sqrt 2 {x^2} + 2{x^3} = 0\) .

Giải

a) \({2 \over 3}x\left( {{x^2} - 4} \right) = 0\)

    \({2 \over 3}x\left( {{x^2} - {2^2}} \right) = 0\)

     \({2 \over 3}x\left( {x - 2} \right)\left( {x + 2} \right) = 0\)

Hoặc \(x = 0\)

Hoặc \(x – 2 = 0 \Rightarrow x = 2\)

Hoặc \(x + 2 = 0 \Rightarrow   x = -2\)

Vậy \(x = 0,x =  - 2,x = 2\)

b) \({\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\)

     \(\left( {x + 2} \right)\left[ {\left( {x + 2} \right) - \left( {x - 2} \right)} \right] = 0\)

     \(\left( {x + 2} \right)\left( {x + 2 - x + 2} \right) = 0\)

     \(\left( {x + 2} \right).4 = 0\)

    \(x + 2 = 0\)

    \(x =  - 2\)

Vậy \(x=-2\) 

c) \(x + 2\sqrt 2 {x^2} + 2{x^3} = 0\)

    \(x\left( {1 + 2\sqrt 2 x + 2{x^2}} \right) = 0\)

    \(x(1^2 + 2\sqrt 2 x .1+ {\left( {\sqrt 2 x} \right)^2}) = 0\)

    \(x{\left( {1 + \sqrt 2 x} \right)^2} = 0\)

Hoặc \(x = 0\)

Hoặc \({\left( {1 + \sqrt 2 x} \right)^2} = 0  \Rightarrow 1 + \sqrt 2 x = 0\Rightarrow  x =  - {1 \over {\sqrt 2 }}\)

Vậy \(x = 0,x =  - {1 \over {\sqrt 2 }}\)

Bài 82 trang 33 sgk toán 8 tập 1

Chứng minh:

a) \({x^2} - 2xy + {y^2} + 1 > 0\)  với mọi số thực \(x\) và \(y\);

b) \(x - {x^2} - 1 < 0\)  với mọi số thực \(x\).

Giải

a) \({x^2} - 2xy + {y^2} + 1 > 0\)  với mọi số thực \(x\) và \(y\)

Ta có \({x^2} - 2xy + {y^2} + 1 = \left( {{x^2} - 2xy + {y^2}} \right) + 1\)

=\({\left( {x - y} \right)^2} + 1 > 0\) do \({\left( {x - y} \right)^2} \ge 0\) với mọi \(x, y\).

b) \(x - {x^2} - 1 < 0\)  với mọi số thực \(x\).

Ta có \(x - {x^2} - 1 =  - \left( {{x^2} - x + 1} \right)\)

=\( - \left[ {{x^2} - 2.x.{1 \over 2} + {{\left( {{1 \over 2}} \right)}^2} + {3 \over 4}} \right]\)

= \( - \left[ {{x^2} - 2x.{1 \over 2} + {{\left( {{1 \over 2}} \right)}^2}} \right] - {3 \over 4}\)

=\( - {\left( {x - {1 \over 2}} \right)^2} - {3 \over 4} < 0\)  với mọi \(x\)

do \({\left( {x - {1 \over 2}} \right)^2} \ge 0\) nên \(-{\left( {x - {1 \over 2}} \right)^2} \le 0\)

Bài 83 trang 33 sgk toán 8 tập 1

Tìm \(n \in\mathbb Z\)  để  \(2{n^2} - n + 2\)  chia hết cho \(2n +1\).

Giải

Ta có: \({{2{n^2} - n + 2} \over {2n + 1}} = {{2{n^2} + n - 2n - 1 + 3} \over {2n + 1}}\)

=\({{n\left( {2n + 1} \right) - \left( {2n + 1} \right) + 3} \over {2n + 1}} = {{\left( {2n + 1} \right)\left( {n - 1} \right) + 3} \over {2n + 1}} = n - 1 + {3 \over {2n + 1}}\)

Để \(2{n^2} - n + 2\) chia hết cho \(2n  + 1\) (với \(n \in\mathbb Z)\) thì \(2n + 1\) phải là ước của \(3\). Do đó:

\(2n + 1 = 1 =  > 2n = 0 =  > n = 0\)

\(2n + 1 =  - 1 =  > 2n =  - 2 =  > n =  - 1\) 

\(2n + 1 = 3 =  > 2n = 2 =  > n = 1\)

\(2n + 1 =  - 3 =  > 2n =  - 4 =  > n =  - 2\)

Vậy \(n = 0; -1; -2; 1\)

Giaibaitap.me