Bài 29 trang 74 - Sách giáo khoa toán 8 tập 2
Cho tam giác ABC và A'B'C' có kích thước như trong hình 35.
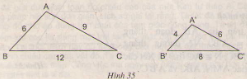
a) Tam giác ABC và A'B'C' có đồng dạng với nhau không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó.
Giải:
\(\frac{AB}{A'B'}\) = \(\frac{BC}{B'C'}\)= \(\frac{CA}{C'A'}\)= 3/2
=> ∆ABC ∽ ∆A'B'C'
b) \(\frac{C_{ABC}}{C_{A'B'C'}}\)= 3/2
Bài 30 trang 75 - Sách giáo khoa toán 8 tập 2
Tam giác ABC có độ dài các cạnh là AB = 3cm, AC = 5cm, BC = 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 55 cm.
Hãy tính độ dài các cạnh của A'B'C'(làm tròn đến chữ số thập phân thứ hai).
Giải
∆ABC ∽ ∆A'B'C' => \(\frac{AB}{A'B'}\) = \(\frac{BC}{B'C'}\)= \(\frac{CA}{C'A'}\) = \(\frac{C_{ABC}}{C_{A'B'C'}}\)
hay \(\frac{3}{A'B'}\) = \(\frac{7}{B'C'}\) = \(\frac{5}{A'C'}\) = \(\frac{C_{ABC}}{55}\) = \(\frac{3}{11}\)
=> A'B' = 11cm;
B'C' = \(\frac{7.11}{3}\) ≈ 25.67 cm
A'C' = \(\frac{5.11}{3}\) ≈ 18,33 cm
Bài 31 trang 75 - Sách giáo khoa toán 8 tập 2
Cho hai tam giác đồng dạng có tỉ số chu vi là \(\frac{15}{17}\) và hiệu độ dài hai cạnh tương ứng của chúng là 12,5 cm. Tính hai cạnh đó.
Giải
Giả sử ∆A'B'C' ∽ ∆ABC, hiệu độ dài tương ứng của A'B' và AB là 12,5.
Ta có: \(\frac{C_{ABC}}{C_{A'B'C'}}\)= \(\frac{15}{17}\) mà \(\frac{C_{ABC}}{C_{A'B'C'}}\) = \(\frac{AB}{A'B'}\)
=> \(\frac{15}{17}\) = \(\frac{AB}{A'B'}\) => \(\frac{AB}{15}\) = \(\frac{A'B'}{17}\) = \(\frac{ A'B'-AB}{17-15}\) = \(\frac{ 12.5}{2}\) = 6,25 cm
Giaibaitap.me
Giải bài tập trang 77 bài 6 Trường hợp đồng dạng thứ hai Sách giáo khoa toán 8 tập 2. Câu 32: Trên một cạnh của góc xOy...
Giải bài tập trang 79 bài 7 Trường hợp đồng dạng thứ ba Sách giáo khoa toán 8 tập 2. Câu 35: Chứng minh rằng nếu tam giác ...
Giải bài tập trang 79, 80 bài 7 Trường hợp đồng dạng thứ ba Sách giáo khoa toán 8 tập 2. Câu 39: Cho hình thang ABCD(AB//CD)...
Giải bài tập trang 80 bài 7 Trường hợp đồng dạng thứ ba Sách giáo khoa toán 8 tập 2. Câu 43:
