Bài 35 trang 79 - Sách giáo khoa toán 8 tập 2

Chứng minh rằng nếu tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) theo tỉ số \(k\) thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng \(k\).

Giải:

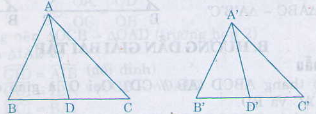
\(∆A'B'C' ∽ ∆ABC\) theo tỉ số \(k= \frac{A'B'}{AB}\)

\( \Rightarrow \widehat {BAC} = \widehat {B'A'C'}\)   (1)

\(AD\) là phân giác góc \(\widehat {BAC}\) nên \(\widehat {BAD} = {1 \over 2}\widehat {BAC}\)     (2)

\(A'D'\) là phân giác góc \(\widehat {B'A'C'}\) nên \(\widehat {B'A'D'} = {1 \over 2}\widehat {B'A'C'}\)   (3)

Từ (1),(2) và (3) suy ra: \(\widehat{BAD}\) = \(\widehat{B'A'D'}\)

Xét \(∆A'B'D'\) và \(∆ABD\) có:

+) \(\widehat{B}\) = \(\widehat{B'}\) 

+) \(\widehat{BAD}\) = \(\widehat{B'A'D'}\)

\(\Rightarrow ∆A'B'D' ∽ ∆ABD\) theo tỉ số \( \frac{A'B'}{AB}\)= \(\frac{A'D'}{AD}=k\)

Bài 36 trang 79 - Sách giáo khoa toán 8 tập 2

Tính độ dài x của đường thẳng BD trong hình 43(Làm tròn đến chữ thập phân thứ nhất), biết rằng ABCD là hinh thang(AD // CD); AB= 12,5cm; CD= 28,5cm

\(\widehat{DAB}\) = \(\widehat{DBC}\).

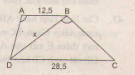
Giải

xét ∆ABD và ∆BDC có:

\(\widehat{DBC}\) = \(\widehat{DBC}\)(gt)

\(\widehat{ABD}\) = \(\widehat{BDC}\)

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> \(\frac{AB}{BD}\) = \(\frac{DB}{DC}\) => BD² = AB.DC

=> BD = √(AB.DC) = √(12,5.8,5) => BD = 10,3 cm

Bài 37 trang 79 - Sách giáo khoa toán 8 tập 2

Hình 44 cho biết \(\widehat{EBA}\) = \(\widehat{BDC}\).

a) Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết AE = 10cm, AB = 15cm, BC = 12cn, Hãy tính độ dài các đoạn thẳng CD, BE, BD, ED(làm tròn đén chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD.

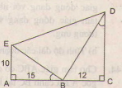
Giải: 

\(\widehat{EBA}\) = \(\widehat{BDC}\).(gt) mà \(\widehat{BCD}\) + \(\widehat{CBD}\) = 90⁰ => \(\widehat{EBA}\) + \(\widehat{CBD}\) = 90⁰

Vậy \(\widehat{EBD}\) = 90⁰

Vậy trong hình vẽ có ba tam giác vuông đó là:

∆ABE, ∆CBD, ∆EBD.

b) ∆ABE và ∆CDB có:

 \(\widehat{A}\) = \(\widehat{C}\) = 90⁰

\(\widehat{ABE}\) = \(\widehat{CDB}\) 

=> ∆ABE ∽ ∆CDB => \(\frac{AB}{CD}\) = \(\frac{AE}{CB}\)

=> CD = \(\frac{AB.CB}{AE}\) = 18 (cm)

 ∆ABE vuông tại A => BE = \(\sqrt{AE^{2}+AB^{2}}\) = \(\sqrt{10^{2}+15^{2}}\) = 21,6 (cm).

∆EBD vuông tại B => ED = \(\sqrt{EB^{2}+BD^{2}}\) = \(\sqrt{325+ 468}\) = 28.2 (cm)

c) Ta có: \(S_{ABE}\) + \(S_{DBC}\) = \(\frac{1}{2}\)AE.AB + \(\frac{1}{2}\)BC.CD 

= \(\frac{1}{2}\). 10.15 + \(\frac{1}{2}\)12.18

= 75 + 108 = 183 cm²

\(S_{ACDE}\)= \(\frac{1}{2}\)(AE + CD).AC

= \(\frac{1}{2}\)(10 + 18).27= 378 cm²

=> \(S_{EBD}\)= \(S_{EBD}\) - (\(S_{ABE}\) + \(S_{DBC}\)) = 378 - 183 = 195cm²

\(S_{EBD}\)> \(S_{ABE}\) + \(S_{DBC}\)

Bài 38 trang 79 - Sách giáo khoa toán 8 tập 2

Tính độ dài x,y của các đoạn thẳng trong hình 45.

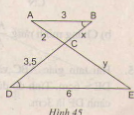
Giải:

\(\widehat{ABD}\) = \(\widehat{BDE}\), lại so le trong

=> AB // DE

=> ∆ABC ∽ ∆EDC

=> \(\frac{AB}{ED}\) = \(\frac{BC}{DC}\) = \(\frac{AC}{EC}\)

=> \(\frac{3}{6}\) = \(\frac{x}{3,5}\) =  \(\frac{2}{y}\)

=> x = \(\frac{3. 3,5}{6}\) = 1.75; 

y = \(\frac{6.2}{3}\) = 4

Giaibaitap.me