Bài 43 trang 80 - Sách giáo khoa toán 8 tập 2

 Cho hình bình hành ABCD(h46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt CB kéo dài tại F,

a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng? hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.

b) Tính độ dài đoạn EF và BF, biết rằng DE = 10cm.

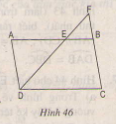
Giải:

a) BE // DC => ∆BEF ∽ ∆CDF

AD // BF => ∆ADE ∽ ∆BFE.

Do đó: ∆ADE ∽ ∆CFD

b) BE = AB - AE = 12 - 8 = 4cm

∆ADE ∽ ∆BFE => \(\frac{AE}{BE}\) = \(\frac{AD}{BF}\) = \(\frac{DE}{EF}\)

=> \(\frac{8}{4}\) = \(\frac{7}{BF}\) = \(\frac{10}{EF}\)

=> BF = 3,5 cm.

EF = 5 cm.

Bài 44 trang 80 - Sách giáo khoa toán 8 tập 2

Cho tam giác ABC có các cạnh AB= 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M,N theo thứ tự là hình chiếu của B và C trên AD.

a) Tính tỉ số \(\frac{BM}{CN}\)

b) Chứng minh rằng \(\frac{AM}{AN}\) = \(\frac{DM}{DN}\)

Giải:

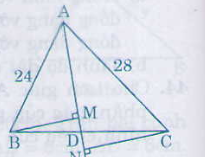
a) AD là đường phân giác của ∆ABC

=> \(\frac{DB}{DC}\) = \(\frac{AB}{AC}\) = \(\frac{DB}{DC}\) = \(\frac{24}{28}\) = \(\frac{6}{7}\)

Mà BM // CN (cùng vuông góc với AD).

=> ∆BMD ∽ ∆CND => \(\frac{BM}{CN}\) = \(\frac{BD}{CD}\) 

Vậy \(\frac{BM}{CN}\) = \(\frac{6}{7}\)

b) ∆ABM và ∆ACN có: \(\widehat{ABM}\) = \(\widehat{CAN}\)

\(\widehat{BMA}\) = \(\widehat{CNA}\) = 90⁰

=> ∆ABM ∽ ∆ACN => \(\frac{AM}{AN}\) = \(\frac{AB}{AC}\).

mà  \(\frac{AB}{AC}\) = \(\frac{DB}{DC}\) (cmt)

và \(\frac{BD}{CD}\) = \(\frac{DM}{DN}\)

=> \(\frac{AM}{AN}\) = \(\frac{DM}{DN}\)

Bài 44 trang 80 sgk toán 8 tập 2

Cho tam giác ABC có các cạnh AB = 24 cm, AC = 28 cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.

a)Tính tỉ số \({{BM} \over {CN}}\).

b)Chứng minh rằng \({{AM} \over {AN}} = {{DM} \over {DN}}\) .

Hướng dẫn làm bài:

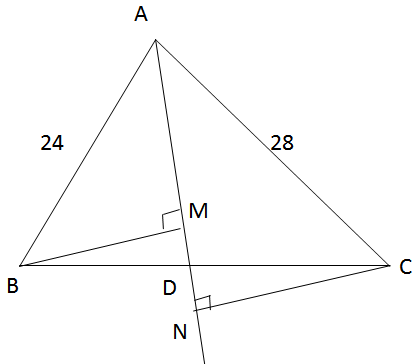
a) AD là đường phân giác trong ∆ABC

=>\({{DB} \over {DC}} = {{AB} \over {AC}} =  > {{DB} \over {DC}} = {{24} \over {28}} = {6 \over 7}\)

Mà BM // CN  (cùng vuông góc với AD).

=>∆BMD ∽ ∆CND =>\({{BM} \over {CN}} = {{BD} \over {CD}}\)

Vậy:\({{BM} \over {CN}} = {6 \over 7}\)

b) ∆ABM và ∆CAN có: \(\widehat {BAM} = \widehat {CAN}\) (AD là phân giác \(\widehat {BAC}\) )

 \(\widehat {BMA} = \widehat {CNA} = {90^0}\)

=>∆ABM ∽∆ACN =>\({{AM} \over {AN}} = {{AB} \over {AC}}\)

Mà \({{AB} \over {AC}} = {{DB} \over {DC}}\) (chứng minh trên)

Và \({{DB} \over {DC}} = {{DM} \over {DN}}\) (∆BMD ∽∆CND)

=>\({{AM} \over {AN}} = {{DM} \over {DN}}\)

Bài 45 trang 80 - Sách giáo khoa toán 8 tập 2

Hai tam giác ABC và DEF có \(\widehat{A}\) = \(\widehat{D}\), \(\widehat{B}\) = \(\widehat{E}\), AB = 8cm, BC = 10cm, DE= 8cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.

Giải:

∆ABC ∽ ∆DEF vì có \(\widehat{A}\) = \(\widehat{D}\), \(\widehat{B}\) = \(\widehat{E}\) nên đồng dạng.

Vì ∆ABC ∽ ∆DEF => \(\frac{AB}{DE}\) = \(\frac{BC}{EF}\) = \(\frac{CA}{FD}\)

Hay \(\frac{8}{6}\) = \(\frac{10}{EF}\) = \(\frac{CA}{FD}\)

Suy ra: EF = 7,5 cm

Vì \(\frac{8}{6}\) = \(\frac{CA}{FD}\) => \(\frac{CA}{8}\) = \(\frac{FD}{6}\) = \(\frac{CA - FD}{8-6}\) = 3/2

=> CD = \(\frac{8.3}{2}\) = 12 cm

FD = 12 -3 = 9cm 

Giaibaitap.me