Bài 23 trang 71 - Sách giáo khoa toán 8 tập 2

 Trong hai mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai?

a) Hai tam giác bằng nhau thì đồng dạng với nhau.

b) Hai tam giác đồng dạng với nhau thì bằng nhau.

Giải: 

a) a là mệnh đề đúng.

b) b là mệnh đề sai 

Bài 24 trang 72 - Sách giáo khoa toán 8 tập 2

∆A'B'C' ∽ ∆A"B"C" theo tỉ số đồng dạng K₁, ∆A"B"C" ∽∆ ABC theo tỉ số đồng dạng k₂. Hỏi tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số nào?

Giải:

 ∆A'B'C' ∽ ∆A"B"C" theo tỉ số đồng dạng K₁ = \(\frac{A'B'}{A"B"}\)

 ∆A"B"C" ∽∆ ABC theo tỉ số đồng dạng k₂ =  \(\frac{A"B"}{AB}\)

Theo tính chất 3 thì ∆A'B'C' ∽ ∆ABC.

Theo tỉ số K= \(\frac{A'B'}{AB}\) = \(\frac{A'B'.A"B"}{A'B'.AB}\) = \(\frac{A'B'}{A"B"}\).\(\frac{A"B"}{AB}\)

vậy K= K₁.k₂

Bài 25 trang 72 - Sách giáo khoa toán 8 tập 2

 Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số \(\frac{1}{2}\).

Giải:

Lấy trung điểm M của AB, N là trung điểm của AC => MN là đường trung bình của tam giác ABC.

=> MN // BC.

=> ∆ AMN ∽  ∆ABC theo tỉ số K = 1/2.

Bài 26 trang 72 - Sách giáo khoa toán 8 tập 2

Cho tam giác ABC vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng là K = \(\frac{2}{3}\)

Giải:

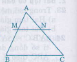
Trên cạnh AB lấy điểm M sao cho AM= \(\frac{2}{3}\)AB.

Từ m kẻ đường song song với AB cắt AC tại N.

Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=\(\frac{2}{3}\)

Dựng  ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)

Bài 27 trang 72 - Sách giáo khoa toán 8 tập 2

Từ M thuộc cạnh AB của tam giác ABC với AM= 1/2 MB. Kẻ các tia song song với AC, BC. Chúng cắt BC và AC lần lượt tại L và N.

a) Nêu tất cả các cặp tam giác đồng dạng.

b) Đối với mỗi cặp tam giác đồng dang, hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng.

Giải:

a) MN // BC => ∆AMN ∽ ∆ABC

ML // AC => ∆MBL ∽ ∆ABC

và ∆AMN ∽ ∆MLB

b) 

∆AMN ∽ ∆ABC có:

\(\widehat{AMN}\) = \(\widehat{ABC}\); \(\widehat{ANM}\) = \(\widehat{ACB}\)

\(\frac{AM}{AB}\)= \(\frac{1}{3}\)

 ∆MBL ∽ ∆ABC có: 

\(\widehat{MBL}\) = \(\widehat{BAC}\), \(\widehat{B}\) chung, \(\widehat{MLB}\) = \(\widehat{ACB}\)

\(\frac{MB}{AB}\)= \(\frac{2}{3}\)

∆AMN ∽ ∆MLB có:

\(\widehat{MAN}\) = \(\widehat{BML}\), \(\widehat{AMN}\) = \(\widehat{MBL}\), \(\widehat{ANM}\) = \(\widehat{MLB}\)

\(\frac{AM}{MB}\) = \(\frac{1}{2}\)

Bài 28 trang 72 - Sách giáo khoa toán 8 tập 2

∆A'B'C' ∽ ∆ABC theo tỉ số đồng dạng K= \(\frac{3}{5}\).

a) Tính tỉ số chú vi của hai tam giác đã cho.

b) Cho biết chu vi của hai tam giác trên là 40dm, tính chu vi của mỗi tam giác.

Giải: 

a)  ∆A'B'C' ∽ ∆ABC theo tỉ số đồng dạng K= \(\frac{3}{5}\).

=> \(\frac{A'B'}{AB}\) = \(\frac{B'C'}{BC}\) = \(\frac{C'A'}{CA}\) = \(\frac{3}{5}\)

Áp dụng tính chất của dãy tỉ số bằng nhau.

=> \(\frac{A'B'}{AB}\)= \(\frac{A'B'+B'C'+C'A'}{AB+CB+CA}\)= \(\frac{C_{A'B'C'}}{C_{ABC}}\)= \(\frac{3}{5}\)

vậy tỉ số chu vi của ∆A'B'C' và ∆ABC là \(\frac{3}{5}\).

b) Vì \(\frac{C_{A'B'C'}}{C_{ABC}}\)= \(\frac{3}{5}\) mà \(C_{ABC}\) - \(C_{A'B'C'}\) = 40dm

=> \(\frac{C_{ABC}}{5}\)= \(\frac{C_{A'B'C'}}{3}\) = \(\frac{40}{2}\) = 20

=> \(C_{ABC}\) = 100 dm

\(C_{A'B'C'}\) = 60 dm

Giaibaitap.me