Bài 19 trang 68 - Sách giáo khoa toán 8 tập 2

Cho hình thang ABCD (AB // CD).

Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự là E và F.

Chứng minh rằng:

a) \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\);      b) \(\frac{AE}{AD}\) = \(\frac{BF}{BC}\)    c) \(\frac{DE}{DA}\) = \(\frac{CF}{CB}\).

Giải:

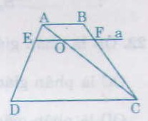
a) Nối AC cắt EF tại O

∆ADC có EO // DC => \(\frac{AE}{ED}\) = \(\frac{AO}{OC}\)       (1)

∆ABC có OF // AB => \(\frac{AO}{OC}\) = \(\frac{BF}{FC}\)         (2)

Từ 1 và 2 => \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\)

b) Từ  \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\) => \(\frac{AE}{ED +AE}\)= \(\frac{BF}{FC + BF}\)

hay  \(\frac{AE}{AD}\)=\(\frac{BF}{BC}\)  

c) Từ \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\)  => \(\frac{AE+ED}{ED}\)= \(\frac{BF+FC}{FC}\)

=> \(\frac{AD}{ED}\) =  \(\frac{BF}{FC}\) hay \(\frac{ED}{AD}\) = \(\frac{FC}{BC}\)

Bài 20 trang 68 - Sách giáo khoa toán 8 tập 2

Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhat tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC théo thứ tự E và F(h26)

Chứng minh rằng OE = OF.

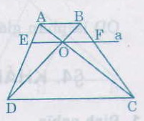
Giải:

∆ADC có OE // OC nên \(\frac{OE}{DC}\) = \(\frac{AE}{AD}\)

∆BDC có OF // DC nên \(\frac{OF}{DC}\) = \(\frac{BF}{BC}\)

Mà AB // CD => \(\frac{AE}{AD}\) = \(\frac{BF}{BC}\)(câu b bài 19)

Vậy \(\frac{OE}{DC}\) = \(\frac{OF}{DC}\) nên OE = OF.

Bài 21 trang 68 - Sách giáo khoa toán 8 tập 2

a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM, biết AB= m, AC= n( n>m). Và diện tích của tam giác ABC là S.

b) Cho n = 7cm, m = 3cm. Hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC.

Giải:

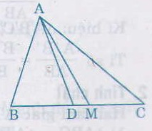
Ta có AD là đường phân giác của ∆ ABC nên

\(\frac{S_{ABD}}{S_{ADC}}\) = \(\frac{AB}{AC}\) = \(\frac{m}{n}\)(kết quả ở bài 16)

=> \(\frac{S_{ABD}}{S_{ADC}+S_{ABD}}\)= \(\frac{m}{n+m}\)

hay \(\frac{S_{ABD}}{S_{ABC}}\)= \(\frac{m}{n+m}\) => \(S_{ABM}\)= \(\frac{1}{2}\) \(S_{ABC}\).

Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.

=> \(S_{ADM}\)= \(S_{ABM}\) - \(S_{ABD}\)

=> \(S_{ADM}\) = \(\frac{1}{2}\)S -\(\frac{m}{n+m}\)S = \(\frac{S(m+n-2m)}{2(m+n)}\)

\(S_{ADM}\)= \(\frac{S(n -m)}{2(m+n)}\) (với n>m)

Bài 22 trang 68 - Sách giáo khoa toán 8 tập 2

 Đố: Hình 27 cho biết có 6 góc bằng nhau:

\(O_{1}\) = \(O_{2}\) = \(O_{3}\) = \(O_{4}\) = \(O_{5}\) = \(O_{6}\).

Kích thước các đoạn thẳng đã được ghi trên hình. Hãy thiết lập những tỉ lệ thức từ kích thước đã cho.

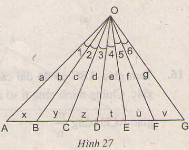
Giải

OB là tia phân giác trong của ∆OBC => \(\frac{x}{a}\) = \(\frac{y}{c}\)

OC là tia phân giác trong của ∆OBD => \(\frac{y}{d}\) = \(\frac{z}{d}\)

OD là tia phân giác trong của ∆OCE => \(\frac{z}{c}\) = \(\frac{t}{e}\)

OE là tia phân giác trong của ∆ODF => \(\frac{t}{d}\) = \(\frac{u}{f}\)

OC là tia phân giác của  ∆ACE => \(\frac{OC}{OA}\) = \(\frac{CE}{OE}\) hay \(\frac{x+ y}{a}\) = \(\frac{z + t}{e}\)

OE là phân giác của ∆OCG => \(\frac{z + t}{c}\) =  \(\frac{u+v }{g}\)

OD  là phân giác của ∆AOG => \(\frac{x+y+x }{a}\) = \(\frac{t+u+v }{g}\)

OD là phân giác của ∆OBF => \(\frac{y+z}{b}\) = \(\frac{t + u}{f}\)

Giaibaitap.me