Bài tập trắc nghiệm khách quan chương III

Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án cho để được khẳng định đúng.

Bài 60 Trang 178 SGK Đại số và Giải tích 12 Nâng cao

Giả sử \(\int\limits_1^5 {{{dx} \over {2x - 1}}}  = \ln c\). Giá trị của c là
(A) \(9\);             (B) \(3\);                 (C) \(81\);                   (D) \(8\).

Giải

\(\eqalign{
& \int\limits_1^5 {{{dx} \over {2x - 1}}} = {1 \over 2}\ln \left| {2x - 1} \right||_1^5 = \ln 3 \cr
& \ln c = \ln 3 \Rightarrow c = 3 \cr} \)

Chọn (B).

Bài 61 Trang 178 SGK Đại số và Giải tích 12 Nâng cao

Giá trị của \(\int\limits_0^2 {2{e^{2x}}dx} \) là

\(\left( A \right)\,{e^4}\);                \(\left( B \right)\,{e^4} - 1;\)

\(\left( C \right)\,4{e^4};\)                \(\left( D \right)\,3{e^4} - 1;\)

Giải

\(\int\limits_0^2 {2{e^{2x}}dx}  = {e^{2x}}|_0^2 = {e^4} - 1\)

Chọn (B).

Bài 62 Trang 178 SGK Đại số và Giải tích 12 Nâng cao

Giá trị của \(\int\limits_{ - 1}^0 {{x^2}{{\left( {x + 1} \right)}^3}dx} \) là:

\(\left( A \right)\, - {7 \over {10}};\)                 \(\left( B \right)\, - {6 \over {10}};\)

\(\left( C \right)\,{2 \over {15}};\)                       \(\left( D \right)\,{1 \over {60}}.\)

Giải

\(\eqalign{
& \int\limits_{ - 1}^0 {{x^2}{{\left( {x + 1} \right)}^3}dx} = \int\limits_{ - 1}^0 {{x^2}\left( {{x^3} + 3{x^2} + 3x + 1} \right)dx} \cr
& = \int\limits_{ - 1}^0 {\left( {{x^5} + 3{x^4} + 3{x^3} + {x^2}} \right)dx}\cr& = \left( {{{{x^6}} \over 6} + {{3{x^5}} \over 5} + {{3{x^4}} \over 4} + {{{x^3}} \over 3}} \right)|_{ - 1}^0 = {1 \over {60}} \cr} \)

Chọn (D).

Bài 63 Trang 178 SGK Đại số và Giải tích 12 Nâng cao

Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bởi đường thẳng \(y = 4x\) và đồ thị hàm số \(y = {x^3}\) là:

(A) \(4\);             (B) \(5\);                 (C) \(3\);                       (D) \(3,5\).

Giải

Phương trình hoành độ giao điểm của hai đồ thị

\(\left\{ \matrix{
{x^3} = 4x \hfill \cr
x \ge 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right.\)

Diện tích cần tìm là:

\(S = \int\limits_0^2 {\left| {4x - {x^3}} \right|dx}  = \int\limits_0^2 {\left( {4x - {x^3}} \right)dx}\)

\(  = \left( {2x^2 - {{{x^4}} \over 4}} \right)|_0^2 = 4\)

Chọn (A).

Bài 64 Trang 178 SGK Đại số và Giải tích 12 Nâng cao

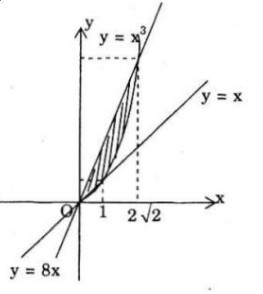
Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bới hai đường thẳng \(y = 8x, y = x\) và đồ thị hàm số \(y = {x^3}\) là:

(A) \(12\);             (B) \(15,75\);            (C) \(6,75\);             (D) \(4\)

Giải

\(\eqalign{
& {x^3} = 8x \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2\sqrt 2 \hfill \cr
x = - 2\sqrt 2 \,\left( \text {loại} \right) \hfill \cr} \right. \cr
& {x^3} = x \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr
x = - 1\,\left( \text {loại} \right) \hfill \cr} \right. \cr} \)

\(\eqalign{
& S =\int\limits_0^{2\sqrt 2 } {\left( {8x - {x^3}} \right)} dx-\int\limits_0^1 {\left( {x - x^3} \right)} dx \cr
& \,\,\,\, = \left( {4{x^2} - {{{x^4}} \over 4}} \right)|_0^{2\sqrt 2 } -\left({1 \over 2}{x^2}-{1 \over 4}{x^4}\right)|_0^1 \cr&= \left( {32 - 16} \right) - \left( {{1 \over 2} - {1 \over 4}} \right) = 16 - {1 \over 4} = 15,75 \cr} \)

Chọn (B).

Bài 65 Trang 178 SGK Đại số và Giải tích 12 Nâng cao

Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bởi đường thẳng \(y=2x\) và đồ thị hàm số \(y = {x^2}\) là:

\(\left( A \right)\,{4 \over 3};\)              \(\left( B \right)\,{3 \over 2};\)

\(\left( C \right)\,{5 \over 3};\)                 \(\left( D \right)\,{{23} \over {15}}.\)

Giải

Phương trình hoành độ giao điểm: 

\(2x = {x^2} \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right.\)

\(S = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx}  = \left( {{x^2} - {{{x^3}} \over 3}} \right)|_0^2 = {4 \over 3}\)

Chọn (A)

Bài 66 Trang 179 SGK Đại số và Giải tích 12 Nâng cao

Cho hình phẳng A được giới hạn bởi đồ thị hàm hai số \(y = {x^2}\) và \(y = 6 - \left| x \right|\). Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung:

\(\left( A \right)\,{{32\pi } \over 3};\)               \(\left( B \right)\,9\pi ;\)

\(\left( C \right)\,8\pi \,;\)                \(\left( D \right)\,{{20\pi } \over 3}.\)

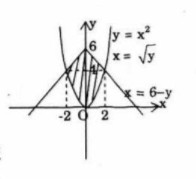
Giải

\(y = 6 - \left| x \right| = \left\{ \matrix{
6 - x\,\,\text{ nếu }\,\,x \ge 0 \hfill \cr
6 + x\,\,\,\text{ nếu }\,\,\,x < 0 \hfill \cr} \right.\)

Giao điểm của (P) với đường thẳng \(y=6-x\) ( với \(x \ge 0\)) là:

\(\left\{ \matrix{
{x^2} = 6 - x \hfill \cr
x \ge 0 \hfill \cr} \right. \Leftrightarrow x = 2\,\left( {y = 4} \right)\)

\(\eqalign{
& V = {\int\limits_0^4 {\pi \left( {\sqrt y } \right)} ^2}dy + \int\limits_4^6 {\pi {{\left( {6 - y} \right)}^2}dy} \cr&= \pi \int\limits_0^4 {ydy} + \pi \int\limits_4^6 {{{\left( {y - 6} \right)}^2}dy} \cr
& = \pi {{{y^2}} \over 2}|_0^4 + \pi {1 \over 3}{\left( {y - 6} \right)^3}|_4^6 = 8\pi + {{8\pi } \over 3} = {{32\pi } \over 3} \cr} \)

Chọn (A)

Bài 67 Trang 179 SGK Đại số và Giải tích 12 Nâng cao

Cho \(a,b\) là hai số dương. Gọi \(K\) là hình phẳng nằm trong góc phần tư thứ hai được giới hạn bởi parabol \(y = a{x^2}\) và đường thẳng \(y=-bx\). Biết rằng thể tích khối tròn xoay tạo được khi quay \(K\) xung quanh trục hoành là một số không phụ thuộc vào giá trị của \(a\) và \(b\). Khi đó \(a\) và \(b\) thỏa mãn điều kiện sau:

\(\left( A \right)\,{b^4} = 2{a^5}\,;\)                     \(\left( B \right)\,{b^3} = 2{a^5}\,;\)

\(\left( C \right)\,{b^5} = 2{a^3}\,;\)                         \(\left( D \right)\,{b^4} = 2{a^2}.\)

Giải

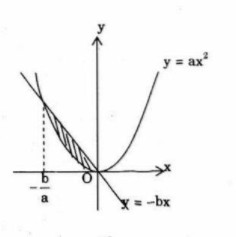
\(a{x^2} = - bx \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = - {b \over a} \hfill \cr} \right.\)

\(V = \pi \int\limits_{ - {b \over a}}^0 {{{\left( { - bx} \right)}^2}} dx - \pi \int\limits_{ - {b \over a}}^0 {{{\left( {a{x^2}} \right)}^2}dx} \)

\(= \pi \int\limits_{ - {b \over a}}^0 {\left( {{b^2}{x^2} - {a^2}{x^4}} \right)} dx =\pi \left( {{{{b^2}{x^3}} \over 3} - {{{a^2}{x^5}} \over 5}} \right)\mathop |\nolimits_{ - {b \over a}}^0 \)

\(=  - \pi \left( {{{ - {b^5}} \over {3{a^3}}} + {{{b^5}} \over {5{a^3}}}} \right) = {{2\pi {b^5}} \over {15{a^3}}}\)

Vì \({{{b^5}} \over {{a^3}}}\) là hằng số nên ta phải chọn (C).

Khi đó \(V = {{4\pi } \over {15}}.\)

Giaibaitap.me