Bài 53 trang 50 SGK giải tích 12 nâng cao

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {{x + 1} \over {x - 2}}\)
b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại giao điểm \(A\) của đồ thị với trục tung.
c) Viết phương trinh tiếp tuyến của đồ thị song song với tiếp tuyến tại điểm \(A\).

Giải

a) TXĐ: \(D =\mathbb R\backslash \left\{ 2 \right\}\)
Tiệm cận đứng \(x = 2\); tiệm cận ngang \(y = 1\).

\(y' = {{ - 3} \over {{{\left( {x - 2} \right)}^2}}} < 0\) với mọi \(x \ne 2\)

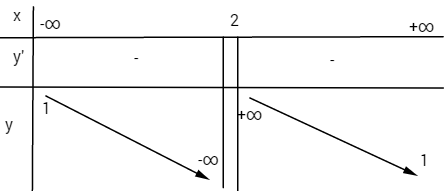
Điểm đặc biệt: \(A\left( {0; - {1 \over 2}} \right),\,B\left( { - 1;0} \right)\)

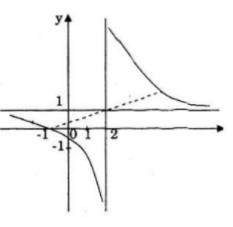
Đồ thị nhận điểm \(I(2;1)\) làm tâm đối xứng.

b) Giao điểm của đồ thị với trục tung \(A\left( {0; - {1 \over 2}} \right)\)

\(y'\left( 0 \right) =  - {3 \over 4}\)

Phương trình tiếp tuyến của đồ thị tại \(A\) là: 

\(y + {1 \over 2} =  - {3 \over 4}\left( {x - 0} \right) \Leftrightarrow y =  - {3 \over 4}x - {1 \over 2}\)

c) Giả sử \(M\) là tiếp điểm của tiếp tuyến song song với tiếp tuyến tại \(A\) ta có:

\(y'\left( {{x_M}} \right) =  - {3 \over 4} \Leftrightarrow {{ - 3} \over {{{\left( {{x_M} - 2} \right)}^2}}} =  - {3 \over 4} \Leftrightarrow {\left( {{x_M} - 2} \right)^2} = 4\)

\( \Leftrightarrow \left[ \matrix{
{x_M} - 2 = 2 \hfill \cr 
{x_M} - 2 = - 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
{x_M} = 4 \hfill \cr 
{x_M} = 0\,\,(\text{ loại vì }{x_A} = 0) \hfill \cr} \right.\)

\(y\left( 4 \right) = {5 \over 2}\). Vậy \(M\left( {4;{5 \over 2}} \right)\)

Phương trình tiếp tuyến tại điểm \(M\) là: \(y - {5 \over 2} =  - {3 \over 4}\left( {x - 4} \right) \Leftrightarrow y =  - {3 \over 4}x + {{11} \over 2}\)

Bài 54 trang 50 SGK giải tích 12 nâng cao

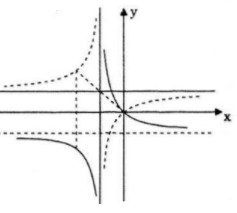
a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số \(y = 1 - {1 \over {x + 1}}\)

b) Từ đồ thị \((H)\) suy ra cách vẽ đồ thị của hàm số \(y = 1 + {1 \over {x + 1}}\)

Giải

a) \(y = {x \over {x + 1}}\)
TXĐ: \(D = R\backslash \left\{ { - 1} \right\}\)
Tiệm cận đứng \(x = -1\); tiệm cận ngang \(y = 1\).

\(y' = {1 \over {{{\left( {x + 1} \right)}^2}}} > 0\) với mọi \(x \ne  - 1\)

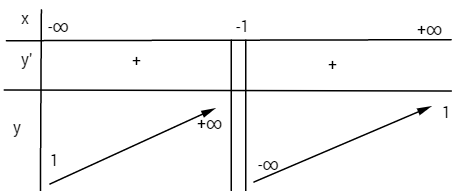
Điểm đặc biệt 

\(\eqalign{
& x = 0 \Rightarrow y = 0 \cr 
& x = 1 \Rightarrow y = {1 \over 2} \cr} \)

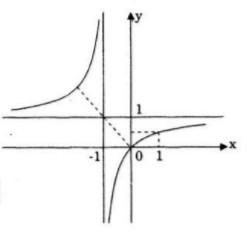
Đồ thị nhận \(I(-1;1)\) làm tâm đối xứng.
b) Ta có \(y =  - 1 + {1 \over {x + 1}} = {{ - x} \over {x + 1}}\)

Do đó đồ thị của hàm số \(y =  - 1 + {1 \over {x + 1}}\) là hình đối xứng của \((H)\) qua trục hoành. 

Bài 55 trang 50 SGK giải tích 12 nâng cao

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = x - {2 \over {x - 1}}\)

b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm \((3;3)\).

Giải

a) Tập xác định: \(D = R\backslash \left\{ 1 \right\}\)

\(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D\)

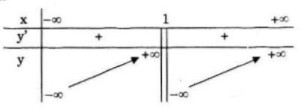
Vậy hàm số đồng biến trên khoảng \(( - \infty ;1)\) và \((1; + \infty )\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \cr 
& \mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \cr} \)

Do đó \(x=1\) là tiệm cận đứng.

\(\mathop {\lim }\limits_{x \to  \pm \infty } (y - x) = \mathop {\lim }\limits_{x \to  \pm \infty } \left( { - {2 \over {x - 1}}} \right) = 0\)

Vậy \(y=x\) là tiệm cận xiên.

Bảng biến thiên:

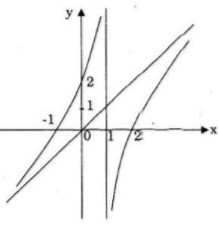
Đồ thị giao \(Ox\) tại \((-1;0),(2;0)\)

Đồ thị giao \(Oy\) tại \(0;2)\)

b) Ta có: \(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}}\)
Phương trình tiếp tuyến với đồ thị hàm số đã cho tại điểm \(M\left( {{x_o};{y_o}} \right) \in \left( C \right)\) là:

\(\left( d \right):\,y - {x_o} + {2 \over {{x_o} - 1}} = \left[ {1 + {2 \over {{{\left( {{x_o} - 1} \right)}^2}}}} \right]\left( {x - {x_o}} \right)\)

\(\left( {x \ne 1} \right)\)

Vì \(\left( {3;3} \right) \in d\) nên \(3 - {x_o} + {2 \over {{x_o} - 1}} = {{{{\left( {{x_o} - 1} \right)}^2} + 2} \over {{{\left( {{x_o} - 1} \right)}^2}}}\left( {3 - {x_o}} \right)\)

\(\eqalign{
& \Leftrightarrow \left( {3 - {x_o}} \right){\left( {{x_o} - 1} \right)^2} + 2\left( {{x_o} - 1} \right)\cr&\,\,\,\, = \left( {{x_o} - 2{x_o} + 3} \right)\left( {3 - {x_o}} \right) \cr 
& \Leftrightarrow {x_o} = 2;\,{y_o} = y\left( 2 \right) = 0 \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y'\left( 2 \right) = 3 \cr} \)

Vậy phương trình tiếp tuyến cần tìm là: \(y = 3\left( {x - 2} \right)\) hay \(y = 3x - 6.\)

Bài 56 trang 50 SGK giải tích 12 nâng cao

a) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số \(y = {{{x^2}} \over {x + 1}}\)

b) Từ đồ thị \((C)\) suy ra cách vẽ đồ thị của hàm số \(y = {{{x^2}} \over {\left| {x + 1} \right|}}\)

Giải

a) \(D = R\backslash \left\{ { - 1} \right\}\)

\(\eqalign{
& y' = {{{x^2} + 2x} \over {{{\left( {x + 1} \right)}^2}}} \cr 
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = - 2 \hfill \cr} \right. \cr} \)

Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\)

Hàm số nghịch biến trên khoảng \((-2;-1)\) và \((1;0)\)

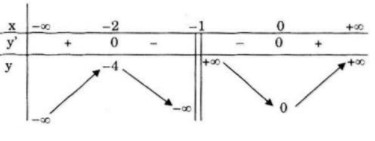
Hàm số đạt cực đại tại \(x=-2\), \(y_{CĐ}=-4\)

Hàm số đạt cực tiểu tại \(x=0\) , \(y_{CT}=0\)

\(\mathop {\lim }\limits_{x \to  - {1^ + }} y =  + \infty \)

\(\mathop {\lim }\limits_{x \to  - {1^ - }} y =  - \infty \)

Vậy \(x=-1\) là tiệm cận đứng.

\(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - (x - 1)} \right] = \mathop {\lim }\limits_{x \to  \pm \infty } \left( {{1 \over {x + 1}}} \right) = 0\)

Vậy \(y=x-1\) là tiệm cận xiên.

Bảng biến thiên

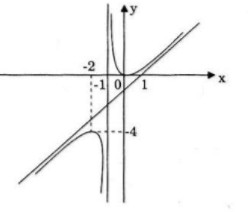
Đồ thị

Đồ thị giao \(Ox\), \(Oy\) tại \(O(0;0)\)

\(x=-2\rightarrow y=-4\)

b) Ta có 

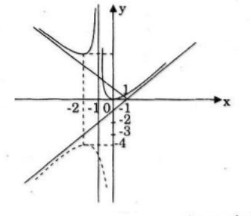
\(y = {{{x^2}} \over {\left| {x + 1} \right|}} = \left\{ \matrix{
{{{x^2}} \over {x + 1}}\,\,\text{nếu} \,x > - 1 \hfill \cr 
- {{{x^2}} \over {x + 1}}\,\,\text{ nếu }\,x < - 1 \hfill \cr} \right.\)

Giữ nguyên phần đồ thị \((C)\) ở bên phải tiệm cận đứng \(x = -1\) và lấy đối xứng của phần \((C)\) bên trái tiệm cận đứng qua trục hoành.

Giaibaitap.me