Bài 4 trang 25 sgk hình học 12

Cho hình chóp $S.ABC$. Trên các đoạn thẳng $SA, SB, SC$ lần lượt lấy ba điểm $A’, B’, C’$ khác với $S$. Chứng minh rằng

${{{V_{S.A'B'C'}}} \over {{V_{S.ABC}}}} = {{SA'} \over {SA}} \cdot {{SB'} \over {SB}} \cdot {{SC'} \over {SC}}$

Giải

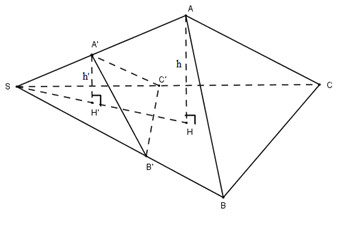
Gọi $h$ và $h’$ lần lượt là chiều cao hạ từ $A, A’$ đến mặt phẳng $(SBC)$.

Gọi $S_1$ và $S_2$ theo thứ tự là diện tích các tam giác $SBC$ và $SB’C’$.

Khi đó ta có ${{h'} \over h} = {{SA'} \over {SA}}$ 

và ${{{1 \over 2}sin(B'SC').SB'.SC'} \over {{1 \over 2}sin(BSC).SB.SC}} = {{SB'} \over {SB}}.{{SC'} \over {SC}}$

Suy ra ${{{V_{S.A'B'C'}}} \over {{V_{S.ABC}}}} = {{{V_{A'.SB'C'}}} \over {{V_{A.SBC}}}} = {{{1 \over 3}h'{S_2}} \over {{1 \over 3}h{S_1}}} = {{SA'} \over {SA}} \cdot {{SB'} \over {SB}} \cdot {{SC'} \over {SC}}$ 

Đó là điều phải chứng minh.

Bài 5 trang 26 sgk hình học 12

Cho tam giác $ABC$ vuông cân ở $A$ và $AB = a$. Trên đường thẳng qua $C$ và vuông góc với mặt phẳng $(ABC)$ lấy điểm $D$ sao cho $CD = a$. Mặt phẳng qua $C$ vuông góc với $SD$, cắt $BD$ tại $F$ và cắt $AD$ tại $E$. Tính thể tích khối tứ diện $CDEF$ theo $a$.

Giải: 

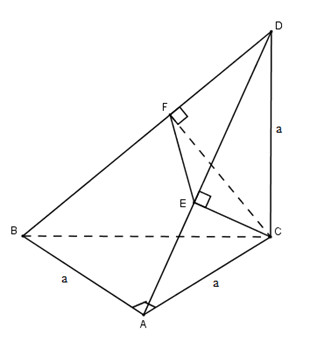
$\left.\begin{matrix} BA \perp CD& \\ BA \perp CA& \end{matrix}\right\}$$\Rightarrow BA\bot (ADC)$ $\Rightarrow BA \bot CE$

Mặt khác $BD \bot (CEF) \Rightarrow BD \bot CE$.

Từ đó suy ra

$CE \bot (ABD) \Rightarrow CE ⊥ EF, CE \bot AD$.

Vì tam giác $ACD$ vuông cân, $AC= CD= a$ nên $CE=\frac{AD}{2}=\frac{a\sqrt{2}}{2}$

Ta có $BC = a\sqrt{2}$, $BD = \sqrt{2a^{2}+a^{2}}=a\sqrt{3}$

Để ý rằng $CF\cdot BD = DC\cdot BC$ nên $CF=\frac{a^{2}\sqrt{2}}{a\sqrt{3}}=a\sqrt{\frac{2}{3}}$

Từ đó suy ra 

$EF= \sqrt{CF^{2}-CE^{2}}=\sqrt{\frac{2}{3}a^{2}-\frac{a^{2}}{2}}=\frac{\sqrt{6}}{6}a$.

$DF=\sqrt{DC^{2}-CF^{2}}=\sqrt{a^{2}-\frac{2}{3}a^{2}}=\frac{\sqrt{3}}{3}a$.

Từ đó suy ra $S_{\Delta CEF}=\frac{1}{2}FE\cdot EC=\frac{1}{2}\frac{a\sqrt{6}}{6}\cdot \frac{a\sqrt{2}}{2}=\frac{a^{2}\sqrt{3}}{12}$

Vậy $V_{D.CEF}=\frac{1}{3}S_{\Delta CEF}\cdot DF=\frac{1}{3}\cdot \frac{a^{2}\sqrt{3}}{12}\cdot \frac{a\sqrt{3}}{3}=\frac{a^{3}}{36}.$

Bài 6 trang 26 sgk hình học 12

Cho hai đường thẳng chéo nhau $d$ và $d’$. Đoạn thằng $AB$ có độ dài $a$ trượt trên $d$, đoạn thẳng $CD$ có độ dài $b$ trượt trên $d’$. Chứng minh rằng khối tứ diện $ABCD$ có thể tích không đổi.

Giải: 

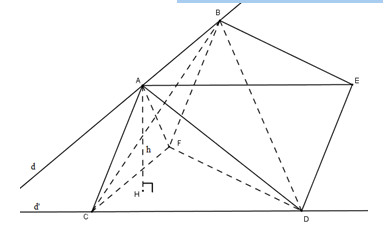
Gọi $h$ là độ dài đường vuông góc chung của $d$ và $d’$, $α$ là góc giữa hai đường thẳng $d$ và $d’$. Qua $B, A, C$ dựng hình bình hành $BACF$. Qua $A,C, D$ dựng hình bình hành $ACDE$.

Khi đó $CFD.ABE$ là một hình lăng trụ tam giác. Ta có:

$V_{DABC}=V_{DFCB}=V_{BCDF}$

= $\frac{1}{3}$$V_{CFD.ABE}$

= $\frac{1}{3}h$$S_{FCD}$= $\frac{1}{3}h.$ $\frac{1}{2}ab. sinα$

=$\frac{1}{6}.h. ab. sinα$ (là một số không đổi).

Giaibaitap.me