Bài 37 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng \(A\) giới hạn bởi các đường \(y = {x^2},x = 0\) và \(x = 2\). Tính thể tích của khối tròn xoay tạo thành khi quay hình \(A\) quanh trục hoành.
Giải
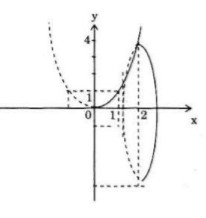
Ta có:
\(V = \pi \int\limits_0^2 {{x^4}dx = \left. {\pi .{{{x^5}} \over 5}} \right|_0^2 = {{32\pi } \over 5}} \)
Bài 38 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng A giới hạn bởi các đường \(y = \cos x, y = 0, x = 0\) và \(x = {\pi \over 4}.\)
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Giải
Ta có:
\(\eqalign{
& V = \pi \int\limits_0^{{\pi \over 4}} {{{\cos }^2}xdx = {\pi \over 2}\int\limits_0^{{\pi \over 4}} {(1 + \cos 2x)dx} } \cr
& = {\pi \over 2}\left. {\left( {x + {1 \over 2}\sin 2x} \right)} \right|_0^{{\pi \over 4}} = {\pi \over 2}\left( {{\pi \over 4} + {1 \over 2}} \right) \cr&= {{\pi (\pi + 2)} \over 8} \cr} \)
Bài 39 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{{x \over 2}}},y = 0,x = 0\) và \(x = 1\).
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Giải
Ta có: \(V = \pi \int\limits_0^1 {{x^2}{e^x}dx} \). Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
\(V = \pi \left( {{x^2}{e^x}\mathop |\nolimits_0^1 - 2\int\limits_0^1 {x{e^x}dx} } \right) = \pi \left( {e - 2{I_1}} \right)\)
Với \({I_1} = \int\limits_0^1 {x{e^x}dx} \). Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Do đó \({I_1} = x{e^x}\mathop |\nolimits_0^1 - \int\limits_0^1 {{e^x}dx = e - {e^x}\mathop |\nolimits_0^1 } = 1\).
Vậy \(V = \pi \left( {e - 2} \right).\)
Bài 40 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt {2\sin 2y} ,x = 0,y = 0\) và \(y = {\pi \over 2}.\)
Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.
Giải
Ta có: \(V = \pi \int\limits_0^{{\pi \over 2}} {2\sin 2ydy = - \pi \cos 2y\mathop |\nolimits_0^{{\pi \over 2}} } = 2\pi \)
Giaibaitap.me
Giải bài tập trang 175, 176 ôn tập chương III - Nguyên hàm, tích phân và ứng dụng SGK Giải tích 12 Nâng cao. Câu 41: Tìm nguyên hàm của các hàm số sau...
Giải bài tập trang 176 ôn tập chương III - Nguyên hàm, tích phân và ứng dụng SGK Giải tích 12 Nâng cao. Câu 45: Xác định số b dương để tích phân sau có giá trị lớn nhất...
Giải bài tập trang 176, 177 ôn tập chương III - Nguyên hàm, tích phân và ứng dụng SGK Giải tích 12 Nâng cao. Câu 49: Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều...
Giải bài tập trang 177 ôn tập chương III - Nguyên hàm, tích phân và ứng dụng SGK Giải tích 12 Nâng cao. Câu 53: Tính thể tích của vật thể nằm giữa hai mặt phẳng...
