Bài 3.39 trang 130 sách bài tập (SBT) – Hình học 12

Cho hai đường thẳng \(\Delta :{{x - 1} \over 2} = {{y + 3} \over 1} = {{z - 4} \over { - 2}}\)

                                 \(\Delta ':{{x + 2} \over { - 4}} = {{y - 1} \over { - 2}} = {{z + 1} \over 4}\)     

a) Xét vị trí tương đối giữa \(\Delta \) và \(\Delta '\) ;

b) Tính khoảng cách giữa \(\Delta \) và \(\Delta '\)  .

Hướng dẫn làm bài:

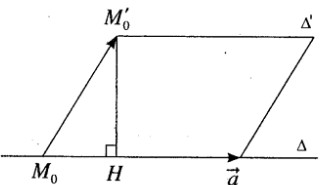
a)  \(\Delta \) đi qua điểm M₀(1; -3; 4) và có vecto chỉ phương \(\overrightarrow a  = (2;1; - 2)\)

\(\Delta '\)   đi qua điểm M₀’ (-2; 1; -1) và có vecto chỉ phương \(\overrightarrow {a'}  = ( - 4; - 2;4)\)

Ta có   \(\left\{ {\matrix{{\overrightarrow {a'} = 2\overrightarrow a } \cr {{M_0} \notin \Delta '} \cr} } \right.\)

Vậy \(\Delta '\)  song song với \(\Delta \)

b) Ta có \(\overrightarrow {{M_0}M{'_0}}  = ( - 3;4; - 5)\)

           \(\overrightarrow a  = (2;1; - 2)\)

\(\overrightarrow n  = \overrightarrow {{M_0}M{'_0}}  \wedge \overrightarrow a  = ( - 3; - 16; - 11)\)

\(d(\Delta ,\Delta ') = M{'_0}H = {{|\overrightarrow n |} \over {|\overrightarrow a |}} = {{\sqrt {9 + 256 + 121} } \over {\sqrt {4 + 1 + 4} }} = {{\sqrt {386} } \over 3}\) 

Bài 3.40 trang 130 sách bài tập (SBT) – Hình học 12

Cho điểm M(2; -1; 1) và đường thẳng \(\Delta :{{x - 1} \over 2} = {{y + 1} \over { - 1}} = {z \over 2}\)

a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng \(\Delta \);

b) Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng \(\Delta \) .

Hướng dẫn làm bài:

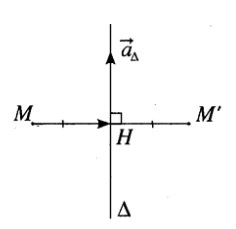
a) Phương trình tham số của \(\Delta :\left\{ {\matrix{{x = 1 + 2t} \cr {y = - 1 - t} \cr {z = 2t} \cr} } \right.\)

Xét điểm \(H(1 + 2t; - 1 - t;2t) \in \Delta \)

Ta có \(\overrightarrow {MH}  = (2t - 1; - t;2t - 1)\)

     \(\overrightarrow {{a_\Delta }}  = (2; - 1;2)\)

H là hình chiếu vuông góc của M trên \(\Delta \Leftrightarrow  \overrightarrow {MH} .\overrightarrow {{a_\Delta }}  = 0\)

\(\Leftrightarrow 2(2t - 1) + t + 2(2t - 1) = 0 \Leftrightarrow t = {4 \over 9}\)

Ta suy ra tọa độ điểm \(H({{17} \over 9};{{ - 13} \over 9};{8 \over 9})\)

b) H là trung điểm của MM’, suy ra x_M’ + x_M = 2x_H

Suy ra \({x_{M'}} = 2{x_H} - {x_M} = {{34} \over 9} - 2 = {{16} \over 9}\)

Tương tự, ta được \({y_{M'}} = 2{y_H} - {y_M} = {{ - 26} \over 9} + 1 = {{ - 17} \over 9};\)

\({z_{M'}} = 2{z_H} - {z_M} = {{16} \over 9} - 1 = {7 \over 9}\)

Vậy  \(M'({{16} \over 9};{{ - 17} \over 9};{7 \over 9})\)

Bài 3.41 trang 131 sách bài tập (SBT) – Hình học 12

Cho điểm M(1; -1; 2) và mặt phẳng \((\alpha )\) : 2x – y + 2z + 12 = 0

a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng \((\alpha )\) ;

b) Tìm tọa độ điểm M’ đối xứng với M qua mặt phẳng \((\alpha )\) .

Hướng dẫn làm bài:

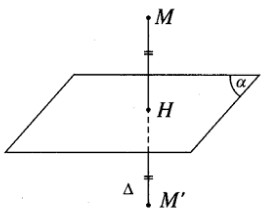
a) Phương trình tham số của đường thẳng \(\Delta \) đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng \((\alpha )\) : 2x – y + 2z + 12 = 0 là:   \(\Delta :\left\{ {\matrix{{x = 1 + 2t} \cr {y = - 1 - t} \cr {z = 2 + 2t} \cr} } \right.\)

Xét điểm H(1 + 2t; -1 – t ; 2 + 2t) \( \in \Delta \)

Ta có \(H \in (\alpha ) \Leftrightarrow 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 \Leftrightarrow t = {{ - 19} \over 9}\)

Vậy ta được \(H({{ - 29} \over 9};{{10} \over 9};{{ - 20} \over 9})\)

b) H là trung điểm của MM’, suy ra \({x_{M'}} = 2{x_H} - {x_M} = {{ - 58} \over 9} - 1 = {{ - 67} \over 9}\)

          \({y_{M'}} = 2{y_H} - {y_M} = {{20} \over 9} + 1 = {{29} \over 9}\)

          \({z_{M'}} = 2{z_H} - {z_M} = {{ - 40} \over 9} - 2 = {{ - 58} \over 9}\)    

Vậy ta được  \(M'({{ - 67} \over 9};{{29} \over 9};{{ - 58} \over 9})\).

Bài 3.42 trang 131 sách bài tập (SBT) – Hình học 12

Cho hai đường thẳng :  \(d:{{x - 1} \over { - 1}} = {{y - 2} \over 2} = {z \over 3}\)  và \(d':\left\{ {\matrix{{x = 1 + t'} \cr {y = 3 - 2t'} \cr {z = 1} \cr} } \right.\)

Lập phương trình đường vuông góc chung của d và d’.

Hướng dẫn làm bài:

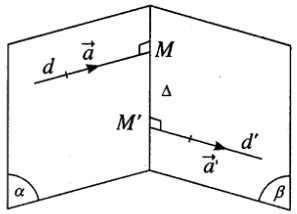
Phương trình tham số của đường thẳng d:\(\left\{ {\matrix{{x = 1 - t} \cr {y = 2 + 2t} \cr {z = 3t} \cr} } \right.\)

Vecto chỉ phương của hai đường thẳng d và d’lần lượt là \(\overrightarrow a  = ( - 1;2;3),\overrightarrow {a'}  = (1; - 2;0)\).

Xét điểm M(1 – t; 2 + 2t; 3t) trên d và điểm M’(1 + t’; 3 – 2t’ ; 1) trên d’ ta có \(\overrightarrow {MM'}  = (t' + t;1 - 2t' - 2t;1 - 3t)\) .

MM’ là đường vuông góc chung của d và d’.

\(\Leftrightarrow \left\{ {\matrix{{\overrightarrow {MM'} .\overrightarrow a = 0} \cr {\overrightarrow {MM'} .\overrightarrow {a'} = 0} \cr} } \right.\)

\(\Leftrightarrow \left\{ {\matrix{{ - t' - t + 2 - 4t' - 4t + 3 - 9t = 0} \cr {t' + t - 2 + 4t' + 4t = 0} \cr} } \right.\)

\( \Leftrightarrow \left\{ {\matrix{{5t' + 14t = 5} \cr {5t' + 5t = 2} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{t = {1 \over 3}} \cr {t' = {1 \over {15}}} \cr} } \right.\)

Thay giá trị của t và t’ vào ta được tọa độ M và M’ là \(M({2 \over 3};{8 \over 3};1),M'({{16} \over {15}};{{43} \over {15}};1)\)

Do đó \(\overrightarrow {MM'}  = ({6 \over {15}};{3 \over {15}};0)\)

Suy ra đường vuông góc chung \(\Delta \) của d và d’ có vecto chỉ phương \(\overrightarrow u  = (2;1;0)\)

Vậy phương trình tham số của \(\Delta \) là: \(\left\{ {\matrix{{x = {2 \over 3} + 2t} \cr {y = {8 \over 3} + t} \cr {z = 1} \cr} } \right.\)

Giaibaitap.me