Bài 2.18 trang 115 Sách bài tập (SBT) Giải tích 12

Hãy so sánh mỗi số sau với 1.

a) \({(0,1)^{\sqrt 2 }}\)                     

b) \({(3,5)^{0,1}}\)                          

c) \({\pi ^{ - 2,7}}\)                                    

d) \({(\frac{{\sqrt 5 }}{5})^{ - 1,2}}\)

Hướng dẫn làm bài:

a) \({(0,1)^{\sqrt 2 }} < 1\)                          

b) \({(3,5)^{0,1}} > 1\)                 

c) \({\pi ^{ - 2,7}} < 1\)                   

d) \({(\frac{{\sqrt 5 }}{5})^{ - 1,2}} > 1\).

Bài 2.19 trang 115 Sách bài tập (SBT) Giải tích 12

Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau:

a) \(y = {2^x}\)  và  y = 8                                                    

b) \(y = {3^x}\)  và \(y = \frac{1}{3}\)

c) \(y = {(\frac{1}{4})^x}\)  và  \(y = \frac{1}{{16}}\)                                              

d) \(y = {(\frac{1}{3})^x}\) và y = 9

Hướng dẫn làm bài:

a)  (3; 8)                       

b) \(( - 1;\frac{1}{3})\)                          

c) \((2;\frac{1}{{16}})\)                          

d) (-2; 9).

Bài 2.20 trang 116 Sách bài tập (SBT) Giải tích 12

Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau:

a) (1,7)³  và 1                                                                       

b) (0,3)²  và 1.

c)  (3,2)^1,5  và (3,2)^1,6                                                           

d)  (0,2)^-3  và (0,2)^-2

e)  \({(\frac{1}{5})^{\sqrt 2 }}\)  và  \({(\frac{1}{5})^{1,4}}\)                                                              

g)  \({6^\pi }\) và 6^3,14              

Hướng dẫn làm bài:

a) (1,7)³  > 1 ;                                             

b) (0,3)²  < 1  ;                           

c) (3,2)^1,5 <  (3,2)^1,6

d) (0,2)^{- 3} > (0,2)^{- 2}                                     

e) \({(\frac{1}{5})^{\sqrt 2 }} < {(\frac{1}{5})^{1,4}}\)                           

g) \({6^\pi } > {6^{3,14}}\).

Bài 2.21 trang 116 Sách bài tập (SBT) Giải tích 12

Từ đồ thị của hàm số \(y = {3^x}\) , hãy vẽ đồ thị của các hàm số sau:

a)  y = 3^x  – 2                                                                           

b) y = 3^x + 2

c) y = |3^x – 2|                                                                           

d) y = 2 – 3^x

Hướng dẫn làm bài:

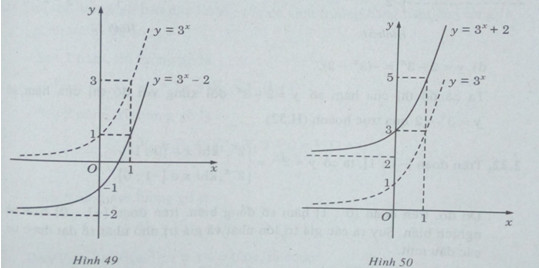
a) Đồ thị của hàm số y \(y = {3^x} - 2\)  nhận được từ đồ thị của hàm số \(y = {3^x}\) bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)

b) Đồ thị của hàm số \(y = {3^x} + 2\) nhận được từ đồ thị của hàm số \(y = {3^x}\) bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)

c) 

\(y = |{3^x} - 2| = \left\{ \begin{array}{l}
{3^x} - 2,{3^x} - 2 \ge 0\\
- {3^x} + 2,{3^x} - 2 < 0
\end{array} \right.\)

Do đó, đồ thị của hàm số \(y = |{3^x} - 2|\) gồm:

- Phần đồ thị của hàm số  \(y = {3^x} - 2\) ứng với \({3^x} - 2 \ge 0\)  (nằm phía trên trục hoành).

- Phần đối xứng qua trục hoành của đồ thị hàm số \(y = {3^x} - 2\)  ứng với \({3^x} - 2 < 0\) .

Vậy đồ thị của hàm số \(y = |{3^x} - 2|\) có dạng như hình 51.

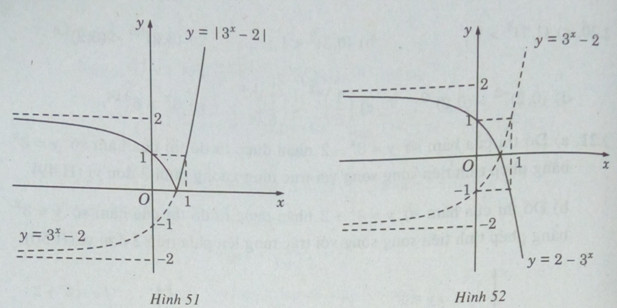
d) \(y = 2 - {3^x} =  - ({3^x} - 2)\)

Ta có đồ thị của hàm số \(y = 2 - {3^x}\) đối xứng với đồ thị cua hàm số \(y = {3^x} - 2\) qua trục hoành (H.52).

Giaibaitap.me