Bài 1 trang 122 SGK Hình học 12 Nâng cao

Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi \(\left( \alpha  \right)\) là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và cắt chúng tại P, Q, R. Phép tịnh tiến theo vectơ \(\overrightarrow {AA'} \) biến tam giác PQR thành tam giác P’Q’R’.
a) Chứng minh rằng thể tích V của hình lăng trụ đã cho bằng thể tích của hình lăng trụ PQR.P’Q’R’.
b) Chứng minh rằng \(V = {S_{PQR}}.AA'\), trong đó \({S_{PQR}}\) là diện tích tam giác PQR.

Giải

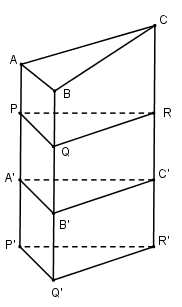
a) Mp(PQR) chia khối lăng trụ ABC.A’B’C’ thành 2 khối đa diện \({H_1}\) và \({H_2}\) với \({H_1}\) chứa \(\Delta ABC\), \({H_2}\) chứa \(\Delta A'B'C'\) Mp(A’B’C’) chia khối lăng trụ PQR.P’Q’R’ thành hai khối đa diện \({H_2}\) và \({H_3}\) với \({H_3}\) chứa \(\Delta P'Q'R'.\)
Gọi \({V_1},{V_2},{V_3}\) lần lượt là thể tích của các khối đa diện \({H_1},{H_2},{H_3}\) ta có:
\({V_{ABC.A'B'C'}} = {V_1} + {V_2},{V_{PQR.P'Q'R'}} = {V_2} + {V_3}.\)
Phép tịnh tiến \(\overrightarrow {AA'} :\)

\(\eqalign{
& {T_{\overrightarrow {AA'} }}:\Delta ABC \to \Delta A'B'C' \cr 
& {T_{\overrightarrow {AA'} }}:\Delta PQR \to \Delta P'Q'R' \cr} \)

Suy ra \({T_{\overrightarrow {AA'} }}:{H_1} \to {H_3}\) do đó \({V_1} = {V_3}.\)
Vậy \({V_{ABC.A'B'C'}} = {V_{PQR.P'Q'R'}}.\)
b) Vì lăng trụ PQR.P’Q’R’ là lăng trụ đứng nên có chiều cao PP’ = AA’ nên

\({V_{ABC.A'B'C'}} = {V_{PQR.P'Q'R'}} = {S_{PQR}}.AA'.\)

Bài 2 trang 122 SGK Hình học 12 Nâng cao

Cho tứ diện ABCD có thể tích V. Hãy tính thể tích hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho.

Giải

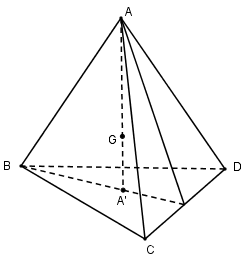
Gọi G là trọng tâm tứ diện ABCD và A’, B’, C’, D’ lần lượt là trọng tâm các tam giác BCD, ACD, ABD, ABC. Gọi \(V\left( {G; - {1 \over 3}} \right)\) là phép vị tự tâm G tỉ số \(k =  - {1 \over 3}.\) Ta có: \(\overrightarrow {GA'}  =  - {1 \over 3}\overrightarrow {GA} .\)

Suy ra: \(V\left( {G; - {1 \over 3}} \right):A \to A'.\)

Tương tự: \(B \to B'\)

                \(\eqalign{
& C \to C' \cr 
& D \to D'. \cr} \)

Do đó: \(V:ABCD \to A'B'C'D'.\) Vậy \({V_{A'B'C'D'}} = {\left| k \right|^3}{V_{ABCD}} = {1 \over {27}}V.\)

Bài 3 trang 122 SGK Hình học 12 Nâng cao

Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Hãy tính thể tích của tứ diện ACB’D’.

Giải

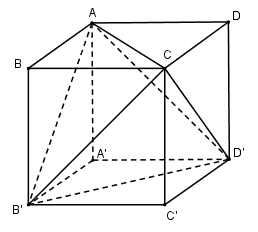
Các tứ diện BACB’, C’B’CD’, DD’AC, AA’B’D’ đều có thể tích bằng \({1 \over 6}V.\)
Do đó: \({V_{ACB'D'}} = V - 4.{V \over 6} = {V \over 3}.\)

Bài 4 trang 122 SGK Hình học 12 Nâng cao

Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình tám mặt đều. Hãy so sánh thể tích của tứ diện đều đã cho và thể tích của hình tám mặt đều đó.

Giải

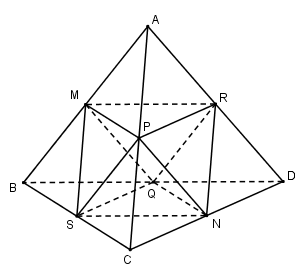
Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, CD, AC, BD, AD, BC của tứ diện đều ABCD thì các tam giác MPR, MRQ, MQS, MSP, NPR, NRQ, NQS, NSP là những tam giác đều, vậy ta có hình tám mặt đều MNPQRS.

Vì các tứ diện AMPR, BMQS, CPSN, DQNR đều là những tứ diện đồng dạng với tứ diện ABCD với tỉ số \(k = {1 \over 2}\) nên ta có thể tích bằng \({V \over 8}.\)

Suy ra \({V_{MPRQSN}} = V - 4{V \over 8} = {V \over 2}.\)

Giaibaitap.me