Bài 1 trang 82 SGK Toán lớp 10 tập 1 Cánh diều:

Cho A, B, C là ba điểm thẳng hàng, B nằm giữa A và C. Viết các cặp vectơ cùng hướng, ngược hướng trong những vectơ sau:  \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {CB} .\)

Lời giải:

Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.

Dễ thấy:

Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)

Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)

Do đó, các cặp vectơ cùng hướng là:

\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \);  \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).

Các cặp vectơ ngược hướng là:

\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);

\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);

\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);

Bài 2 trang 82 SGK Toán lớp 10 tập 1 Cánh diều:

Cho đoạn thẳng MN có trung điểm là I.

a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.

b) vectơ nào bằng \(\overrightarrow {MI} \)?  Bằng \(\overrightarrow {NI} \)?

Phương pháp:

a) Liệt kê các vectơ tạo thành từ 3 điểm M, N, I (điểm đầu và điểm cuối không trùng nhau)

b) Trong các vectơ ở câu a, vectơ nào: Cùng hướng, cùng độ dài với vectơ \(\overrightarrow {MI} \) (tương ứng là \(\overrightarrow {NI} \)).

Lời giải:

a) Các vectơ cần tìm là: \(\overrightarrow {MI} ,\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {NI} ,\overrightarrow {MN} ,\overrightarrow {NM} \).

b) Dễ thấy:

+) vectơ \(\overrightarrow {IN} \)cùng hướng với vectơ \(\overrightarrow {MI} \). Hơn nữa: \(|\overrightarrow {IN} |\; = IN = MI = \;|\overrightarrow {MI} |\)

\( \Rightarrow \overrightarrow {IN}  = \overrightarrow {MI} \)

+) vectơ \(\overrightarrow {IM} \)cùng hướng với vectơ \(\overrightarrow {NI} \). Hơn nữa: \(|\overrightarrow {IM} |\; = IM = NI = \;|\overrightarrow {NI} |\)

\( \Rightarrow \overrightarrow {IM}  = \overrightarrow {NI} \)

Vậy \(\overrightarrow {IN}  = \overrightarrow {MI} \) và \(\overrightarrow {IM}  = \overrightarrow {NI} \).

Bài 3 trang 82 SGK Toán lớp 10 tập 1 Cánh diều:

Cho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:

a) Cùng hướng với \(\overrightarrow {AB} \)

b) Ngược hướng với \(\overrightarrow {AB} \)

Lời giải:

ABCD là hình thang có hai đáy AB và CD nên AB // CD.

Trong các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong bốn điểm A, B, C, D, vectơ ngược hướng với vectơ \(\overrightarrow {AB} \) là vectơ \(\overrightarrow {BA} \) và vectơ \(\overrightarrow {CD} \) (do cùng phương và ngược chiều).

Bài 4 trang 82 SGK Toán lớp 10 tập 1 Cánh diều:

Cho hình vuông ABCD có độ dài cạnh bằng 3cm. Tính độ dài của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \).

Lời giải:

Hình vuông ABCD có cạnh bằng 3 cm nên AB = BC = CD = DA = 3 cm. 

Tam giác ADC vuông tại D (tính chất hình vuông), áp dụng định lí Pythagore, ta có: 

AC² = AD² + DC² = 3² + 3² = 18

\( \Rightarrow \;|\overrightarrow {AC} |\, = 3\sqrt 2 \)

Độ dài vectơ \(\overrightarrow {AB} \) chính là độ dài đoạn thẳng AB nên \(|\overrightarrow {AB} |\, = 3;\) cm. 

Độ dài vectơ \(\overrightarrow {AC} \) chính là độ dài đoạn thẳng AC nên \(|\overrightarrow {AC} |\, = 3\sqrt 2 \) cm. 

Bài 5 trang 82 SGK Toán lớp 10 tập 1 Cánh diều:

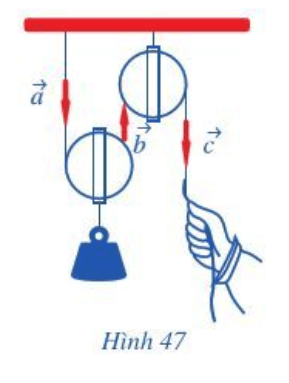
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)(Hình 47).

a) Hãy chỉ ra các cặp vectơ cùng phương.

b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.

Lời giải:

a) Quan sát Hình 47 ta thấy giá của các vectơ \( \Rightarrow \) Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) song song với nhau, do đó các cặp vectơ cùng phương là: 

+ Vectơ \(\overrightarrow a ,\overrightarrow b\); 

+ Vectơ \(\overrightarrow a ,\overrightarrow c \) ; 

+ Vectơ \(\overrightarrow b ,\overrightarrow c \) . 

b) Quan sát hướng mũi tên, ta thấy: 

+ Vectơ \(\overrightarrow a\)  và \(\overrightarrow b\) ngược hướng; 

+ Vectơ \(\overrightarrow a\) và \(\overrightarrow c\) cùng hướng; 

+ Vectơ \(\overrightarrow b\) và \(\overrightarrow c\) ngược hướng.

Giabaitap.me