Bài 9.32 trang 109 SGK Toán 8 Kết nối tri thức tập 2

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH=16cm, CH=9cm

a) Tính độ dài đoạn thẳng AH

b) Tính độ dài đoạn thằng AB và AC

Lời giải:

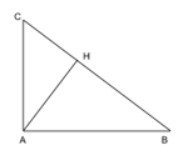
a) Có BC=BH+CH=16+9=25

Xét tam giác AHC vuông tại H có: \(A{H^2} = A{C^2} - C{H^2}\)(định lý Pythagore) (1)

Xét tam giác AHB vuông tại H có: \(A{H^2} = A{B^2} - B{H^2}\) (định lý Pythagore) (2)

Xét (1) + (2), có:

\(\begin{array}{l}2{\rm{A}}{H^2} = A{C^2} - C{H^2} + A{B^2} - B{H^2}\\2{\rm{A}}{H^2} = B{C^2} - C{H^2} - B{H^2}\\2{\rm{A}}{H^2} = {25^2} - {9^2} - {16^2}\\2{\rm{A}}{H^2} = 288\end{array}\)

AH=12(cm)

b) Có \(A{C^2} = A{H^2} + C{H^2}\) (định lý Pythagore) 

=> \(A{C^2} = {12^2} + {9^2} = 225\)

=> AC=15(cm)

Có  \(A{B^2} = A{H^2} + B{H^2}\) (định lý Pythagore) 

=> \(A{B^2} = {12^2} + {16^2} = 400\)

=> AB=20(cm)

Bài 9.33 trang 109  SGK Toán 8 Kết nối tri thức tập 2

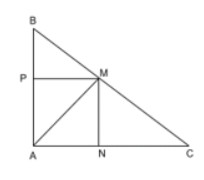
Cho tam giác ABC có AB=6cm, AC=8cm, BC=10cm. Cho điểm M nằm trên cạnh BC sao cho BM=4cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB.

a) Chứng minh ΔBMP ∽ ΔMCN 

b) Tính độ dài đoạn thẳng AM

Lời giải:

Bài 9.34 trang 109 SGK Toán 8 Kết nối tri thức tập 2

Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng

a) ΔAEH ∽ ΔAHB 

b) ΔAFH ∽ ΔAHC 

c) ΔAFE ∽ ΔABC 

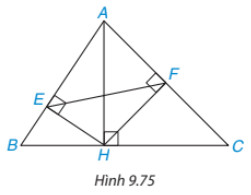
Lời giải:

a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có: góc A chung

=> ΔAEH ∽ ΔAHB 

b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có: góc A chung

ΔAFH ∽ ΔAHC 

c) Vì ΔAEH ∽ ΔAHB nên:

\(\frac{{A{\rm{E}}}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow A{\rm{E}} = \frac{{A{H^2}}}{{AB}}\) (1)

Vì ΔAFH ∽ ΔAHC nên:

\(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF = \frac{{A{H^2}}}{{AC}}\)(2)

Từ (1) và (2) ta có:

\[\frac{{A{\rm{E}}}}{{AF}} = \frac{{AC}}{{AB}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\]

Xét hai tam giác ΔAFE và ΔABC có:

Góc A chung

\[\frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\]

Suy ra ΔAFE ∽ ΔABC (c.g.c)

Bài 9.35 trang 109 SGK Toán 8 Kết nối tri thức tập 2

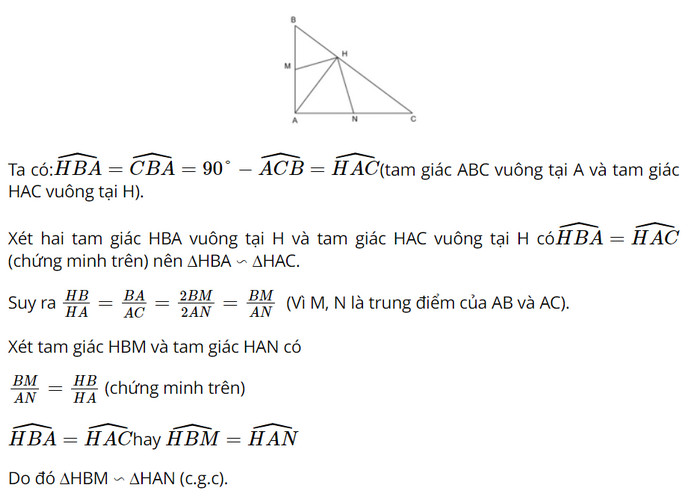
Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM ∽ ΔHAN 

Lời giải:

Bài 9.36 trang 109 SGK Toán 8 Kết nối tri thức tập 2

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3m

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3m, hỏi bóng cột cờ dài bao nhiêu mét? 

Lời giải:

a) Gọi x là độ cao của cột đèn, có: \(\frac{{0,6}}{3} = \frac{{1,4}}{x}\)

=> x=7m

b) Gọi y là độ dài bóng cột cờ, có \(\frac{3}{y} = \frac{{1,4}}{7}\)

=> y=15m

Giaibaitap.me