Bài 63 trang 100 sgk toán 8 tập 1

Tìm \(x\) trên hình 90.

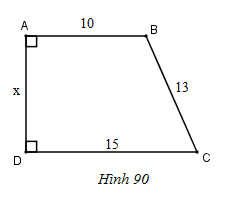
Bài giải:

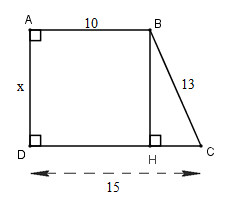
Kẻ \(BH ⊥ CD\)

Tứ giác \(ABHD\) có \(3\) góc vuông nên là hình chữ nhật.

Suy ra \(DH =AB= 10\)

Nên \(HC = 15-10=5\).

Áp dụng định lí Pytago vào tam giác vuông \(BHC\)

\(\eqalign{
& B{H^2} = B{C^2} - H{C^2} \cr&= {13^2} - {5^2} = 169 - 25 = 144 \cr
& BH = x = \sqrt {144} = 12 \cr} \)

Vậy \(x = 12\).

Bài 64 trang 100 sgk toán 8 tập 1

Cho hình bình hành \(ABCD\). Các tia phân giác của các góc \(A, B, C, D\) cắt nhau như trên hình 91. Chứng minh rằng \(EFGH\) là hình chữ nhật.

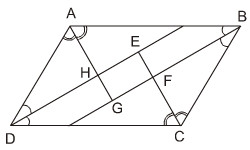
Bài giải:

Theo giả thiết \(ABCD\) là hình bình hành nên theo tính  chất của hình bình hành ta có:

     \(\widehat A = \widehat C,\widehat B = \widehat D\)                                (1)

Theo định lí tổng các góc trong một tứ giác ta có:

     \(\widehat A + \widehat C + \widehat B + \widehat D = {360^0}\)                 (2)

Từ (1) và (2) suy ra: \(\widehat A + \widehat B = {{{{360}^0}} \over 2} = {180^0}\)

\(AG\) là tia phân giác góc \(\widehat A\) nên ta có: \(\widehat {BAG} = {1 \over 2}\widehat A\)

\(BG\) là tia phân giác góc \(\widehat B\) nên ta có: \(\widehat {ABG} = {1 \over 2}\widehat B\)

Do đó: \(\widehat {BAG} + \widehat {ABG} = {1 \over 2}\left( {\widehat A + \widehat B} \right) = {1 \over 2}{.180^0} = {90^0}\)

Xét tam giác \(AGB\) có: \(\widehat {BAG} + \widehat {ABG} = {90^0}\)       (3)

Theo định lí tổng ba góc trong một tam giác ta có:

     \(\widehat {BAG} + \widehat {ABG} + \widehat {AGB} = {180^0}\)                       (4)

Từ (3) và (4) suy ra: \(\widehat {AGB} = {90^0}\)        

Chứng minh tương tự ta được: \(\widehat {DEC} = \widehat {EHG} = {90^0}\)

Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật.

Bài 65 trang 100 sgk toán 8 tập 1

Tứ giác \(ABCD\) có hai đường chéo vuông góc với nhau. Gọi \(E, F, G, H\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CD, DA\). Tứ giác \(EFGH\) là hình gì ? Vì sao ?

Bài giải:

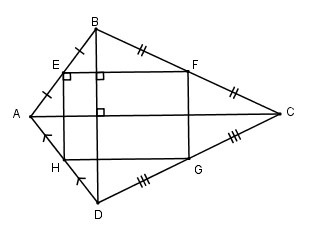
Ta có \(EB = EA, FB = FC\) (do \(E,F\) là trung điểm của \(AB,BC\))

\(EF\) là đường trung bình của \(∆ABC\)

Do đó \(EF // AC\)  (1)

Do \(G,H\) là trung điểm của \(CD,DA) nên

\( HG\) là đường trung bình của \(∆ADC\)

Do đó \(HG // AC\)  (2)

Từ (1) và (2) suy ra \(EF // HG\)

Chứng minh tương tự \(EH // FG\)

Do đó \(EFGH\) là hình bình hành.

Ta có: \(EF // AC\) và \(EH//BD\) mà \(AC\bot BD\) nên \(EF\bot EH\)

Hay \(\widehat{FEH} = 90^0\)

Hình bình hành \(EFGH\)  có \(\widehat{E} = 90^0\) nên là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật).

Bài 66 trang 100 sgk toán 8 tập 1

 Đố. Một đội công nhân đang trồng cây trên đoạn đường \(AB\) thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm \(C, D, E\) như trên hình vẽ rồi trồng cây tiếp trên đoạn thẳng \(EF\) vuông góc với \(DE\). Vì sao \(AB\) và \(EF\) cùng nằm trên một đường thẳng ?

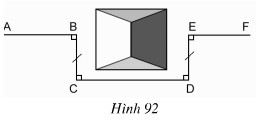
Bài giải:

Tứ giác \(BCDE\) có:

         \(BC // DE\) (vì cùng vuông góc với \(CD\))

        \(BC = DE\) (giả thiết)

        \(\widehat {BCD} = \widehat {EDC} = {90^0}\)

do đó \(BCDE\) là hình chữ nhật

Suy ra: \(\widehat {CBE} = \widehat {BED} = {90^0}\)

Mặt khác: \(\widehat {CBA} = \widehat {FED} = {90^0}\) (giả thiết)

Ta có: \(\widehat {CBA} + \widehat {CBE} = {90^0} + {90^0} = {180^0}\)

Suy ra \(A,B,E\) thẳng hàng

\(\widehat {FED} + \widehat {BED} = {90^0} + {90^0} = {180^0}\)

Suy ra \(B,E,F\) thẳng hàng

Vậy \(AB\) và \(EF\) cùng nằm trên một đường thẳng.

Giaibaitap.me