Bài 55 trang 128 sgk toán 8 tập 2.

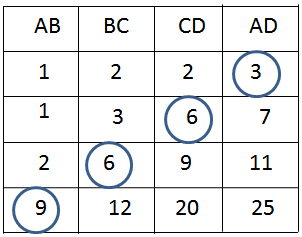
A, B, C, D là các đỉnh của một hình hộp chữ nhật. Hãy quan sát hình 145 rồi điền số thích hợp vào các ô trống ở bảng sau:

Hướng dẫn làm bài:

Ở ô (I):\(AD = \sqrt {A{B^2} + B{C^2} + C{D^2}}\)

\( = \sqrt {{1^2} + {2^2} + {2^2}}  = \sqrt 9  = 3\)

Ở ô (II):\(BD = \sqrt {A{D^2} - A{B^2}}  = \sqrt {{7^2} - {2^2}}  = \sqrt {45} \)

 \(CD = \sqrt {B{D^2} - B{C^2}}  = \sqrt {45 - {3^2}}  = \sqrt {36}  = 6\)

Ở ô (III):\(BD = \sqrt {A{D^2} - A{B^2}}  = \sqrt {{{11}^2} - {2^2}}  = \sqrt {117} \)

 \(BC = \sqrt {B{D^2} - D{C^2}}\)

\( = \sqrt {117 - {9^2}}  = \sqrt {117 - 81}  = \sqrt {36}  = 6\)

Ở ô (IV):\(BD = \sqrt {D{C^2} + B{C^2}}\)

\( = \sqrt {{{20}^2} + {{12}^2}}  = \sqrt {400 + 144}  = \sqrt {544} \)

 \(AB = \sqrt {A{D^2} - B{D^2}}  = \sqrt {{{25}^2} - 544}  = \sqrt {81}  = 9\)

Vậy ta được kết quả ở bảng sau:

Bài 56 trang 129 sgk toán 8 tập 2

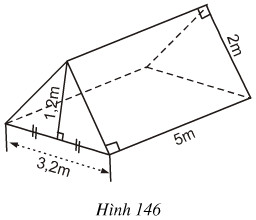
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146).

a)Tính thể tích khoảng không ở bên trong lều.

b)Số vài bạt cần có để dựng lều đó là bao nhiêu?

(Không tính các mép và nếp gấp của lều).

Hướng dẫn làm bài:

a) Lều là lăng trụ đứng tam giác.

Diện tích đáy (tam giác):

\(S = {1 \over 2}.3,2.1,2 = 1,92\left( {{m^2}} \right)\)

Thể tích khoảng không bên trong lều là:

V = Sh = 1,92. 5 = 9,6 (m³)

b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.

Diện tích xung quanh lăng trụ là:

S_xq = 2ph = (2 + 2+ 3,2) .5 = 36 (m²)

Diện tích toàn phần:

S_tp = S_xq + 2S_đ = 36 + 2.1,92 = 39,84 (m²)

Diện tích mặt bên kích thước 5m và 3,2m là:

S = 5.3,2 = 16 (m²)

Vậy số vải bạt cần có để dựng lều là:

39,84 – 16 = 23,84 (m²)

Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.

Bài 57 trang 129 sgk toán 8 tập 2

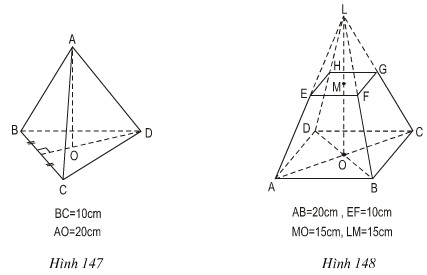
Tính thể tích của hình chóp đều, hình chóp cụt đều sau đây (h.147 và h.148), (.

Hướng dẫn: Hình chóp L.EFGH cũng là hình chóp đều

Hướng dẫn làm bài:

a) Hình 147

Chiều cao của tam giác đều BCD cạnh 10 cm là:

 \(DH = {{10\sqrt 3 } \over 2} = 5\sqrt 3  \approx 8,65\left( {cm} \right)\)

Diện tích đáy của hình chóp:

 \(S = {1 \over 2}.BC.DH = {1 \over 2}.10.8,65 = 43,25\left( {c{m^2}} \right)\)

Thể tích hình chóp đều:

 \(V = {1 \over 3}.S.h = {1 \over 3}.43,25.20 = 288,33(c{m^3})\)

b) Hình 148

Thể tích của hình chóp cụt đều chính là hiệu của thể tích hình chóp đều L.ABCD với thể tích của hình chóp đều L.EFGH. Do có LO = LM + MO = 15 + 15 = 30 (cm)

+Tính thể tích hình chóp đều L.ABCD:

-Diện tích đáy: S = AB² = 20² = 400 (cm²)

-Thể tích : \(V = {1 \over 3}Sh = {1 \over 3}.400.30 = 4000\left( {c{m^3}} \right)\)

+Thể tích hình chóp đều L.EFGH:

-Diện tích đáy: S = EF² = 10² = 100 (cm²)

-Thể tích:\(V = {1 \over 3}Sh = {1 \over 3}.100.15 = 500\left( {c{m^3}} \right)\)

Vậy thể tích hình chóp cụt đều là:

V = 4000 – 500 = 3500 (cm³)

Bài 58 trang 129 sgk toán 8 tập 2

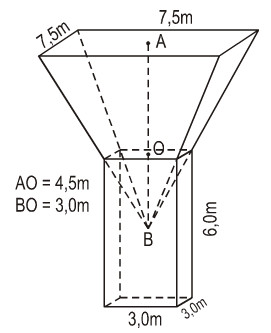
Tính thể tích của hình cho trên hình 150 với các kích thước kèm theo.

Hướng dẫn làm bài:

Thể tích cần tính bao gồm một hình hộp chữ nhật và một hình chóp cụt.

V_hộp = 3.3.6 = 54 (m³)

Thể tích hình chóp với đường cao:

BA = BO + OA = 3,0 + 4,5 = 7,5

 \({V_1} = {1 \over 3}Sh = {1 \over 3}.7,5.7,5.7,5 = 140,625\left( {{m^3}} \right)\)

Thể tích hình chóp với đường cao BO = 3,0 m

 \({V_2} = {1 \over 3}.S.h = {1 \over 3}.3.3.3 = 9\left( {{m^3}} \right)\)

Thể tích hình chóp cụt:

V_c = V₁ – V₂ = 140,625 – 9 = 131,625 (m²)

Thể tích cần tính là:

V = V_hộp + V_c = 54 + 131,625 = 185,62 (m²)

Giaibaitap.me