Bài 54 trang 96 sgk toán 8 tập 1

Cho góc vuông \(xOy\), điểm \(A\) nằm trong góc đó. Gọi \(B\) là điểm đối xứng với \(A\) qua \(Ox\), gọi \(C\) là điểm đối xứng với \(A\) qua \(Oy\). Chứng mình rằng điểm \(B\) đối xứng với điểm \(C\) qua \(O\).

Bài giải:              

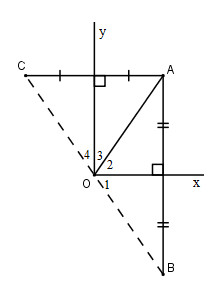
\(A\) đối xứng với \(B\) qua \(Ox\) và \(O\) nằm trên \(Ox\) nên \(OA\) đối xứng với \(OB\) qua \(Ox\) suy ra \(OA = OB\).  (1)

Tam giác \(AOB\) cân tại \(O\) nên \(\widehat O_1=\widehat O_2\)   (3)

\(A\) đối xứng với \(C\) qua \(Oy\) và \(O\) nằm trên \(Oy\) nên \(OA\) đối xứng với \(OC\) qua \(Oy\) suy ra \(OA = OC\)           (2)

Tam giác \(AOC\) cân tại \(O\) nên \(\widehat O_3=\widehat O_4\)    (4)

Từ (1) và (2) suy ra \(OB = OC\)           (*)

Từ (3) và (4) suy ra \(\widehat O_1+\widehat O_2+\widehat O_3+\widehat O_4=2(\widehat O_2+\widehat O_3)=2.90^0=180^0\) 

Do đó \(B, O, C\) thẳng hàng   (2*)

Từ (*) và (2*) suy ra \(B\) đối xứng với \(C\) qua \(O\).

Bài 55 trang 96 sgk toán 8 tập 1

 Cho hình bình hành \(ABCD\), \(O\) là giao điểm của hai đường chéo. Một đường thẳng đi qua \(O\) cắt các cạnh \(AB\) và \(CD\) theo thứ tự ở \(M\) và \(N\). Chứng minh rằng điểm \(M\) đối xứng với điểm \(N\) qua \(O\).

Bài giải:

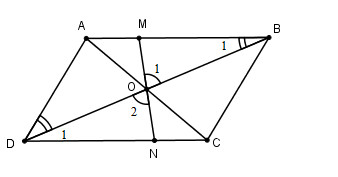
Xét tam giác \(BOM\) và \(DON\) có

+) \(\widehat{B_{1}}\) = \(\widehat{D_{1}}\) (so le trong)

+) \(BO = DO\) (tính chất hình bình hành)

+) \(\widehat{O_{1}}\) = \(\widehat{O_{2}}\) (đối đỉnh) 

Suy ra:\( ∆BOM = ∆DON (g.c.g)\)

Suy ra \(OM = ON\) (hai cạnh tương ứng).

Do đó \(O\) là trung điểm của \(MN\) nên \(M \) đối xứng với \(N\) qua \(O\).

Bài 56 trang 96 sgk toán 8 tập 1

Trong các hình vẽ sau, hình nào có tâm đối xứng ?

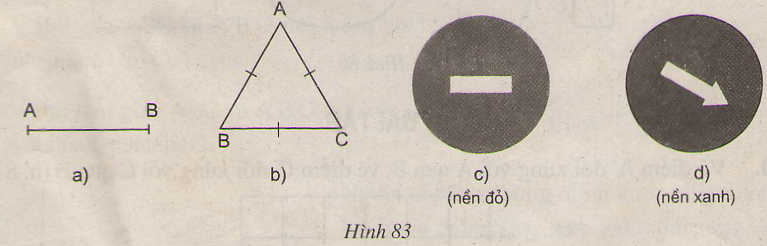
a) Đoạn thẳng \(AB\) (h.83a);

b) Tam giác đếu \(ABC\) (h.83b);

c) Biển cấm đi ngược chiều (h.83c);

d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.83d)

Bài giải:

Hình 83a, c có tâm đối xứng.

Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng \(AB\),

Hình 83c có tâm đối xứng là tâm của đường tròn.

Bài 57 trang 96 sgk toán 8 tập 1

Các câu sau đúng hay sai ?

a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.

b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.

c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.

Bài giải:

a) Đúng, vì nếu lấy một điểm \(O\) bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai tia và với bất kì một điểm \(M\), trên tia này cũng luôn có một điểm \(M'\) đối xứng với nó qua \(O\) trên tia kia.

b) Sai, vì nếu lấy điểm đối xứng của đỉnh \(A\) của tam giác qua trọng tâm thì điểm đối xứng này không nằm trên tam giác.

c) Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau. (Hai tam giác bằng nhau có chu vi bằng nhau).

Giaibaitap.me