Bài 46 trang 57 sách giáo khoa toán 8 tập 1

Biến đổi mỗi biểu thức sau thành một phân thức đại số:

a) $\frac{1+\frac{1}{x}}{1-\frac{1}{x}}$;                

b) $\frac{1-\frac{2}{x+1}}{1-\frac{x^{2}-2}{x^{2}-1}}$.

Hướng dẫn giải:

a) $\frac{1+\frac{1}{x}}{1-\frac{1}{x}}$ $=(1+\frac{1}{x}):(1-\frac{1}{x})$

$= \frac{x+1}{x}:\frac{x-1}{x}=\frac{x+1}{x}.\frac{x}{x-1}=\frac{x+1}{x-1}$

b) $\frac{1-\frac{2}{x+1}}{1-\frac{x^{2}-2}{x^{2}-1}}$ $=(1-\frac{2}{x+1}):(1-\frac{x^{2}-2}{x^{2}-1})$

                       $=\frac{x+1-2}{x+1}:\frac{x^{2}-1-(x^{2}-2)}{x^{2}-1}$

                       $=\frac{x-1}{x+1}:\frac{x^{2}-1-x^{2}+2}{x^{2}-1}=\frac{x-1}{x+1}:\frac{1}{(x-1)(x+1)}$

                        $=\frac{x-1}{x+1}.\frac{(x-1)(x+1)}{1}= (x-1)^{2}$.

Bài 47 trang 57 sách giáo khoa toán 8 tập 1

Với giá trị nào của x thì giá trị của mỗi phân thức sau được xác định?

a) $\frac{5x}{2x+4}$;                        b) $\frac{x-1}{x^{2}-1}$.

Hướng dẫn giải:

a) Giá trị của phân thức này được xác định với điều kiện $2x + 4 \ne 0$

$=> 2x \ne -4$ hay $x \ne -2$

Vậy điều kiện để phân thức $\frac{5x}{2x+4}$ được xác định với $x \ne -2$

b) Điều kiện để phân thức xác định là x² - 1 $\ne$ 0 hay (x - 1)(x + 1) $\ne$ 0.

Do đó $x - 1 \ne 0$ và $x + 1 \ne 0$ hay $x \ne1$ và $x \ne -1$

Vậu điều kiện để phân thức $\frac{x-1}{x^{2}-1}$ được xác định là $x \ne 1$ và $x \ne -1$ 

Bài 48 trang 58 sách giáo khoa toán 8 tập 1

Cho phân thức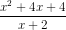 

a) Với điều kiện nào của x thì giá trị của phân thức được xác định?

b) Rút gọn phân thức?

c) Tìm giá trị của x để giá trị của phân thức bằng 1

d) Có giá trị nào của x để giá trị của phân thức bằng 0 hay không?

Hướng dẫn giải:

a) Điều kiện của x để phân thức được xác định là:

x + 2 $\ne$ 0 => x$\ne$ -2

b) Rút gọn phân thức: 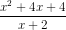 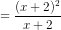 = x + 2

c) Nếu giá trị của phân thức đã cho bằng 1 thì x + 2 = 1

Do đó x = -1. Giá trị này thoả mãn với giá trị của x.

d) Nếu giá trị của phân thức đã cho bằng 0 thì x + 2 = 0 => x = -2.

Giá trị này không thoả mãn với điều kiện của x ( x $\ne$ -2). Vây không có giá trị nào của x để biểu thức đã cho có giá trị bằng 0 

Bài 49 trang 58 sách giáo khoa toán 8 tập 1

Đố. Đố em tìm được một phân thức ( của một biến x) mà giá trị của nó tìm được xác định với mọi giá trị của x khác các ước của 2. 

Hướng dẫn giải:

Các ước của 2 là +1, -1, +2, -2.

(x + 1)(x - 1)(x + 2)(x - 2) $\ne$ 0 khi x $\ne$ $\pm$1, x $\ne$ $\pm$2.

Vậy có thể chọn phân thức $\frac{1}{(x+1)(x-1)(x+2)(x-2)}$

Bài 50 trang 58 sgk toán 8 tập 1

Thực hiện các phép tính:

a)$\left( {{x \over {x + 1}} + 1} \right):\left( {1 - {{3{x^2}} \over {1 - {x^2}}}} \right);$

b)$\left( {{x^2} - 1} \right)\left( {{1 \over {x - 1}} - {1 \over {x + 1}} - 1} \right)$

Hướng dẫn làm bài:

a)$\left( {{x \over {x + 1}} + 1} \right):\left( {1 - {{3{x^2}} \over {1 - {x^2}}}} \right) = {{x + 1 + 1} \over {x + 1}}:{{1 - {x^2} - 3{x^2}} \over {1 - {x^2}}}$

$= {{2x + 1} \over {x + 1}}:{{1 - 4{x^2}} \over {1 - {x^2}}} = {{2x + 1} \over {x + 1}}.{{1 - {x^2}} \over {1 - 4{x^2}}}$

$= {{2x + 1} \over {x + 1}}.{{\left( {1 - x} \right)\left( {1 + x} \right)} \over {\left( {1 - 2x} \right)\left( {1 + 2x} \right)}} = {{1 - x} \over {1 - 2x}}$

b)$\left( {{x^2} - 1} \right)\left( {{1 \over {x - 1}} - {1 \over {x + 1}} - 1} \right)$

$= \left( {{x^2} - 1} \right).\left[ {{{x + 1 - \left( {x - 1} \right) - \left( {x - 1} \right)\left( {x + 1} \right)} \over {\left( {x - 1} \right)\left( {x + 1} \right)}}} \right]$

$= \left( {{x^2} - 1} \right).{{x + 1 - x + 1 - {x^2} + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = \left( {{x^2} - 1} \right).{{3 - {x^2}} \over {\left( {x - 1} \right)\left( {x + 1} \right)}}$

$= {{\left( {x - 1} \right)\left( {x + 1} \right)\left( {3 - {x^2}} \right)} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = 3 - {x^2}$

Giaibaitap.me