Bài 56 trang 92 sgk toán 8 tập 2

Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:

a)AB = 5cm, CD = 15 cm;

b)AB = 45 dm, CD = 150 cm;

c)AB = 5CD.

Giải

a)AB  = 5cm và CD = 15cm =>\({{AB} \over {CD}} = {5 \over {15}} = {1 \over 3}\)

b)AB = 45dm = 450cm và CD = 150 cm

=>\({{AB} \over {CD}} = {{450} \over {150}} = 3\)

c)AB = 5CD =>\({{AB} \over {CD}} = 5\)

Bài 57 trang 92 sgk toán 8 tập 2

Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.

Giải

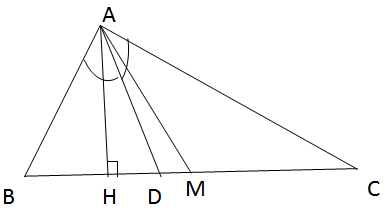
+Nhận xét: D luôn nằm giữa H và M.

+Chứng minh: AD là đường phân giác của ∆ABC.

=>\({{AB} \over {AC}} = {{DB} \over {DC}}\)  AB < AC

=>DB < DC => DB + DC < DC + DC

=>BD + DC < 2DC hay BC < 2DC => DC >\({{BC} \over 2}\)

Mà \(MC = {{BC} \over 2}\) (M là trung điểm của BC)

=>DC > MC =>M nằm giữa D và C (1)

+Mặt khác: \(\widehat {CAH} = {90^0} - \hat C\) (∆CAH vuông tại H)

\(\hat A + \hat B + \hat C = {180^0}\) (tổng 3 góc ∆ABC)

=>\(\widehat {CAH} = {{\hat A + \hat B + \hat C} \over 2} - \hat C\)

=>\(\widehat {CAH} = {{\hat A} \over 2} + {{\hat B} \over 2} - {{\hat C} \over 2} = {{\hat A} \over 2} + {{\hat B - \hat C} \over 2}\)

Vì AB < AC =>\(\widehat C < \widehat B \Rightarrow \widehat B - \widehat C > 0\)

Do đó: \(\widehat {CAH} > {{\hat A} \over 2}\) hay \(\widehat {CAH} > \widehat {CAD}\)

=>Tia AD nằm giữa hai tia AH và AC =>D nằm giữa hai điểm H và C (2)

Từ (1) và (2) => D nằm giữa H và M.

Bài 58 trang 92 sgk toán 8 tập 2

Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (H.66).

a)Chứng minh BK = CH.

b)Chứng minh KH//BC.

c)Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.

Hướng dẫn câu c):

-Vẽ thêm đường cao AI, xét hai tam giác đồng dạng IAC và HBC rồi tính CH.

-Tiếp theo, xét hai tam giác đồng dạng AKH và ABC rồi tính HK.

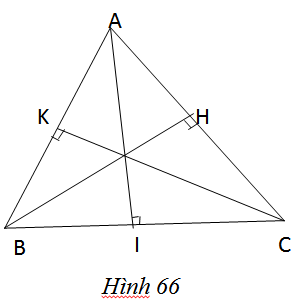
Giải

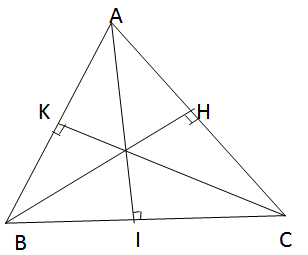
a)Xét hai tam giác vuông BKC và CHB có:

\(\widehat {KBC} = \widehat {HCB}\) (∆ABC cân tại A)

BC là cạnh chung

=>∆BKC = ∆CHB

=>BK = CH

b)Ta có : AB = AC (∆ABC cân tại A)

BK = CH (∆BKC = ∆CHB) => AK = AH

Do đó : \({{AK} \over {AB}} = {{AH} \over {AC}}\) =>KH // BC (định lí Ta lét đảo)

c)BH cắt CK tại M =>M là trực tâm của ∆ABC

=>AM ⊥ BC tại I.

Ta có : ∆AIC ∽ ∆BHC vì \(\left\{ {\matrix{{\hat I = \hat H = {{90}^0}} \cr {\hat Cchung} \cr} } \right.\)

=>\({{IC} \over {HC}} = {{AC} \over {BC}}hay{{{a \over 2}} \over {HC}} = {b \over a} =  > HC = {{{a^2}} \over {2b}}\)

=>\(AH = b - {{{a^2}} \over {2b}} = {{2{b^2} - {a^2}} \over {2b}}\)

Mà HK // BC => \({{HK} \over {BC}} = {{AH} \over {AC}} =  > HK = {{BC.AH} \over {AC}}\)

=>\(HK = {a \over b}\left( {{{2{b^2} - {a^2}} \over {2b}}} \right) = {{2a{b^2} - {a^2}} \over {2{b^2}}}\)

Bài 59 trang 92 sgk toán 8 tập 2

Hình thang ABCD (AB//CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.

Giải

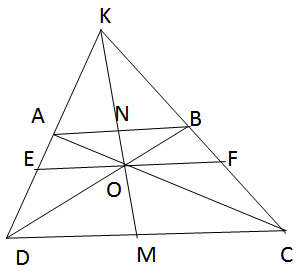
Qua O kẻ đường thẳng song song với AB, CD cắt AD, BC lần lượt tại E, F.

Ta có: OE = OF (xem cách chứng minh ở bài tập 20)

Do đó: \({{AN} \over {EO}} = {{KN} \over {KO}}\) (AN // EO)

Mà \({{BN} \over {OF}} = {{KN} \over {KO}}\) (BN // OF)

=>\({{AN} \over {EO}} = {{BN} \over {FO}}\) Mà OE = OF

=>AN = BN hay N là trung điểm của AB.

Chứng minh tương tự: \({{DM} \over {OE}} = {{CM} \over {OF}} =  > MD = MC\)

=>M là trung điểm của CD.

Bài 60 trang 92 sgk toán 8 tập 2

Cho tam giác vuông ABC,  và đường phân giác BD (D thuộc cạnh AC).

a)Tính tỉ số .

b)Cho biết độ dài AB = 12,5 cm, hãy tính chu vi và diện tích của tam giác ABC.

Giải

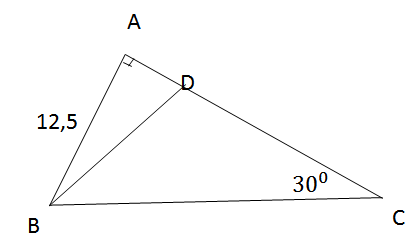
a)Tam giác BCA vuông tại A có  nên là một nửa tam giác đều

=>\({{AB} \over {BC}} = {1 \over 2}\)

Vì BD là đường phân giác của ∆ABC nên: \({{DA} \over {DC}} = {{BA} \over {BC}}\)

b)∆ABC vuông tại A nên AC² = BC² – AB², BC = 2AB

=>AC² = 4AB² – AB² = 3AB²

=>AC=\(\sqrt {3A{B^2}}  = AB\sqrt 3  = 12,5\sqrt 3  \approx 21,65\left( {cm} \right)\)

Gọi p là chu vi ∆ABC =>p = AB + BC + CA

=>p = 3AB + AC = 3.12,5 + 12,5\(\sqrt 3 \)

=>p = 12,5 (3+\(\sqrt 3 ) \approx 59,15\left( {cm} \right)\)

Và \({S_{ABC}} = {1 \over 2}AB.AC \approx 135,31(c{m^2})\)

Bài 61 trang 92 sgk toán 8 tập 2

Tứ giác ABCD có AB = 4cm, BC = 20 cm, CD = 25 cm, DA = 8cm, đường chéo BD = 10cm.

a)Nêu cách vẽ tứ giác ABCD có kích thước đã cho ở trên.

b)Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao?

c)Chứng minh rằng AB // CD.

Giải

a)Vẽ ∆DBC biết BD = 10 cm, BC = 20 cm, DC = 25 cm.

Trên nửa mặt phẳng bờ BD không chứa C vẽ hai cung tròn tâm B và tâm D bán kính lần lượt là 4 cm và 8 cm. Hai cung này cắt nhau tại A.

Vẽ các đoạn BA, DA được tứ giác ABCD.

b)Ta có: \({{AB} \over {BD}} = {4 \over {10}} = {2 \over 5};{{BD} \over {DC}} = {{10} \over {25}} = {2 \over 5};{{AD} \over {BC}} = {8 \over {20}} = {2 \over 5}\)

=>\({{AB} \over {BD}} = {{BD} \over {DC}} = {{AD} \over {BC}} =  > \Delta ABD\Delta BDC\)

c)∆ABD∽ ∆BDC =>\(\widehat {ABD} = \widehat {BDC}\) lại so le trong.

=>AB // DC hay ABCD là hình thang.

Giaibaitap.me