Bài 43 trang 92 sgk toán 8 tập 1

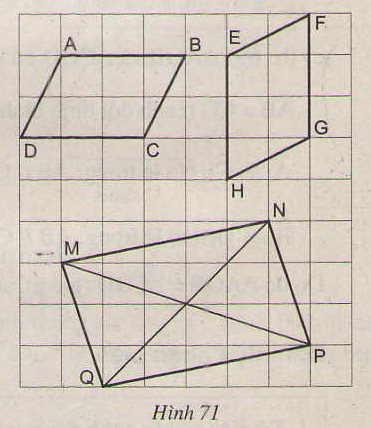
Các tứ giác \(ABCD, EFGH, MNPQ\)
trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không ?

Bài giải:

Cả ba tứ giác là hình bình hành.

- Tứ giác \(ABCD\) là hình bình hành vì có

\(AB // CD\) và \(AB = CD =3\) (theo dấu hiệu nhận biết số 3)

- Tứ giác \(EFGH\) là hình bình hành vì có

\(EH // FG\) và \(EH = FH = 3\)  (theo dấu hiệu nhận biết 3)

- Tứ giác \(MNPQ\) là hình bình hành vì có \(MN = QP\) và \(MQ = NP\) ( theo dấu hiệu nhận biết số 2)

Bài 44 trang 92 sgk toán 8 tập 1

Cho hình bình hành \(ABCD\). Gọi  \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\). Chứng minh rằng \(BE = DF\).

Bài giải:

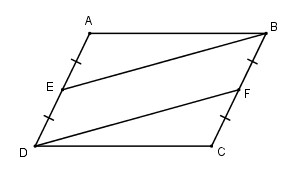
Tứ giác \(BEDF\) có:

\(DE // BF\) và \(AD=BC\) ( vì \(ABCD\) hình bình hành)

\(E\) là trung điểm của \(AD\) nên \(DE = \frac{1}{2}AD\)

\(F\) là trung điểm của \(BC\) nên \(BF= \frac{1}{2}BC\) 

Mà \(AD=BC\) nên \(DE=BF\)

Tứ giác \(BEDF\) có \(DE//BF\) và \(DE=BF\) nên \(BEDF\) là hình bình hành (theo dấu hiệu nhận biết hình bình hành).

Suy ra \(BE = DF\). (tính chất hình bình hành)

Bài 45 trang 92 sgk toán 8 tập 1

Cho hình bình hành \(ABCD\) (\(AB > BC\)). Tia phân giác của góc \(D\) cắt \(AB\) ở \(E\), tia phân giác của góc \(B\) cắt \(CD\) ở \(F\).

a) Chứng minh rằng \(DE // BF\).

b) Tứ giác \(DEBF\) là hình gì ? Vì sao ?

Bài giải:

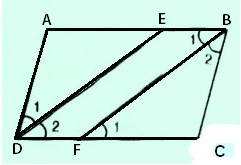
a) Ta có :

\(\widehat B = \widehat D\) (Vì \(ABC  D\) là hình hành)                       (1)

\(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{B \over 2}}\) (vì \(BF\) là tia phân giác góc \(B\))    (2)

\(\widehat {{D_1}} = \widehat {{D_2}} = {{\widehat D} \over 2}\) (vì \(DE\) là tia phân giác góc \(D\))   (3)

Từ (1), (2), (3) \(\Rightarrow \widehat {{D_2}} = \widehat {{B_1}}\) mà hai góc này ở vị trí so le trong do đó: \(DE//BF\)   (*)

b) Ta lại có \(AB // CD\) (Vì \(ABCD\) là hình bình hành) nghĩa là \(BE // DF\)         (2*)

Từ (*) và (2*) ta có tứ giác \(DEBF\) là hình bình hành.

Bài 46 trang 92 sgk toán 8 tập 1

Các câu sau đúng hay sai ?
a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành.
b) Hình thang có hai cạnh bên song song là hình bình hành.

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành.

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành.

Bài giải:

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bàng nhau nên là hình bình hành theo dấu hiệu nhận biết 5.

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa).

c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành.

d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 47 trang 93 sgk toán 8 tập 1

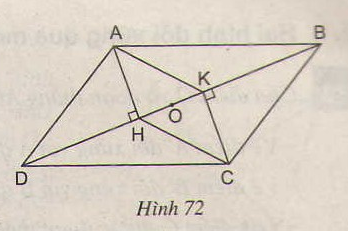
Cho hình 72, trong đó \(ABCD\) là hình bình hành.

a) Chứng minh rằng \(AHCK\) là hình bình hành.

b) Gọi \(O\) là trung điểm của \(HK\). Chứng minh rằng ba điểm \(A, O, C\) thẳng hàng

Bài giải:

a) Xét hai tam giác vuông \(AHD\) và \(CKB\) có:

          \( AD = CB\) (vì \(ABCD\) là hình bình hành)

         \(\widehat {ADH} = \widehat {CBK}\) (hai góc ở vị trí so le trong)

Suy ra \(∆AHD =  ∆CKB\) (cạnh huyền- góc nhọn)

Suy ra \(AH = CK\)

\(AH\bot BD\) và \(CK\bot BD\) suy ra \(AH//CK\)

Tứ giác \(AHCK\) có \(AH//CK\) và \(AH = CK\) nên là hình bình hành (theo dấu hiệu nhận biết hình bình hành),

b) Xét hình bình hành \(AHCK\) có \(O\) là trung điểm của \(HK\), do đó \(O\) là giao điểm của hai đường chéo \(AC\) và \(HK\) của hình bình hành.

Hay \(A,O,C\) thẳng hàng

Bài 48 trang 93 sgk toán 8 tập 1

Tứ giác ABCD có E, F, G, H theo thứ tự là trung  điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?

Bài giải:

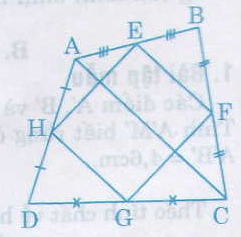
Tứ giác EFGH là hình bình hành.

Cách 1: EB = EA, FB = FC (gt)

nên EF là đường trung bình của ∆ABC.

Do đó EF // AC

Tương tự HG là đường trung bình của ∆ACD.

Do đó HG // AC

Suy ra EF // HG       (1)

Tương tự EH // FG   (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).

Cách 2: EF là đường trung bình của ∆ABC nên EF = \(\frac{1}{2}\)AC.

HG là đường trung bình của ∆ACD nên HG = \(\frac{1}{2}\)AC.

Suy ra EF = HG

Lại có EF // HG ( chứng minh trên)

Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3).

Bài 49 trang 93 sgk toán 8 tập 1

Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Bài giải:

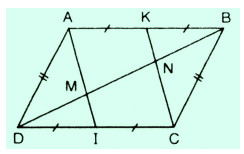
a) Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.

Tứ giác AICK có AK // IC, AK = IC nên là AICK hình bình hành.

Do đó AI // CK

b) ∆DCN có DI = IC, IM // CN.

(vì AI // CK) nên suy ra DM = MN   (1)

 ∆ABM có AK = KB và KN // AM ( vì AI // CK ) nên MN = NB.   (2)

Từ (1) và (2) suy ra DM = MN = NB

Giaibaitap.me