Bài 5.5 trang 219 sách bài tập (SBT) - Giải tích 12

Tìm các điểm cực trị của các hàm số sau:

a) \(y =  - {x^3} - 6{x^2} + 15x + 1\)                 b) \(y = {x^2}\sqrt {{x^2} + 2} \)

c) \(y = x + \ln (x + 1)\)                               d) \(y = x - 1 + {1 \over {x + 1}}\)

Hướng dẫn làm bài

a) \(y' =  - 3{x^2} - 12x + 15;y'' =  - 6x - 12\)

\(y' = 0\Leftrightarrow 3{x^2} + 12x - 15 = 0 \Leftrightarrow \left[ {\matrix{{x = 1} \cr {x = - 5} \cr} } \right.\)

 \(y''(1) =  - 18 < 0;y''( - 5) = 18 > 0\)

Vậy với x = -5 hàm số đạt cực tiểu và yCT = -99

        Với x = 1 hàm số đạt cực đại và yCĐ = 9

b) Tập xác định  D = R. Hàm số có cực tiểu khi x = 0, yCT = 0

c) Tập xác định: \(x >  - 1;y' = 1 + {1 \over {x + 1}};y' > 0,\forall x >  - 1\)

Hàm số luôn đồng biến nên không có cực trị.

d) Tập xác định:  R\{-1}; 

\(y' = 1 - {1 \over {{{(x + 1)}^2}}};y' = 0\Leftrightarrow \left[ {\matrix{{x = 0} \cr {x = - 2} \cr} } \right.\)

\(y'' = {2 \over {{{(x + 1)}^3}}};y''(0) = 2 > 0'y''( - 2) =  - 2 < 0\)        

Hàm số đạt cực đại tại x = -2 và y_CĐ = - 4

Hàm số đạt cực tiểu tại x = 0 và y_CT = 0

Bài 5.6 trang 219 sách bài tập (SBT) - Giải tích 12

Tìm \(a \in (0;2\pi )\) để hàm số  \(y = {1 \over 3}{x^3} - {1 \over 2}(1 + 2\cos a){x^2} + 2x\cos a + 1\)  đồng biến trên khoảng \((1; + \infty )\).

Hướng dẫn làm bài

Tập xác định:  D = R;  \(y' = {x^2} - (1 + 2\cos a)x + 2\cos a\)

              \(y' = 0  \Leftrightarrow  \left[ {\matrix{{x = 1} \cr {x = 2\cos a} \cr} } \right.\)

Vì y’ > 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì \(2\cos a \le 1  \Leftrightarrow  \cos a \le {1 \over 2} \Rightarrow {\pi  \over 3} \le a \le {{5\pi } \over 3}\)   (vì \(a \in (0;2\pi )\) ).

Bài 5.7 trang 220 sách bài tập (SBT) - Giải tích 12

Chứng minh các bất đẳng thức sau:

a) \({e^x} + \cos x \ge 2 + x - {{{x^2}} \over 2},\forall x \in R\)

b) \({e^x} - {e^{ - x}} \ge 2\ln (x + \sqrt {1 + {x^2}} ),\forall x \ge 0\)

c) \(8{\sin ^2}{x \over 2} + \sin 2x > 2x,\forall x \in (0;\pi {\rm{]}}\)

Hướng dẫn làm bài

a) Xét hàm số \(f(x) = {e^x} + \cos x - 2 - x + {{{x^2}} \over 2}\)  , có tập xác định là R.

          \(f'(x) = {e^x} - \sin x - 1 + x;f'(x) = 0  \Leftrightarrow x = 0\)               

Ta lại có  \(f''(x) = {e^x} + 1 - \cos x > 0,\forall x\)  vì \(1 - \cos x \ge 0\)  và \({e^x} > 0\)

Như vậy, f’(x) đồng biến trên R. Từ đó: \(f'(x) < f'(0) = 0,\forall x < 0;f'(x) > f'(0) = 0,\forall x > 0\)

Ta có bảng biến thiên

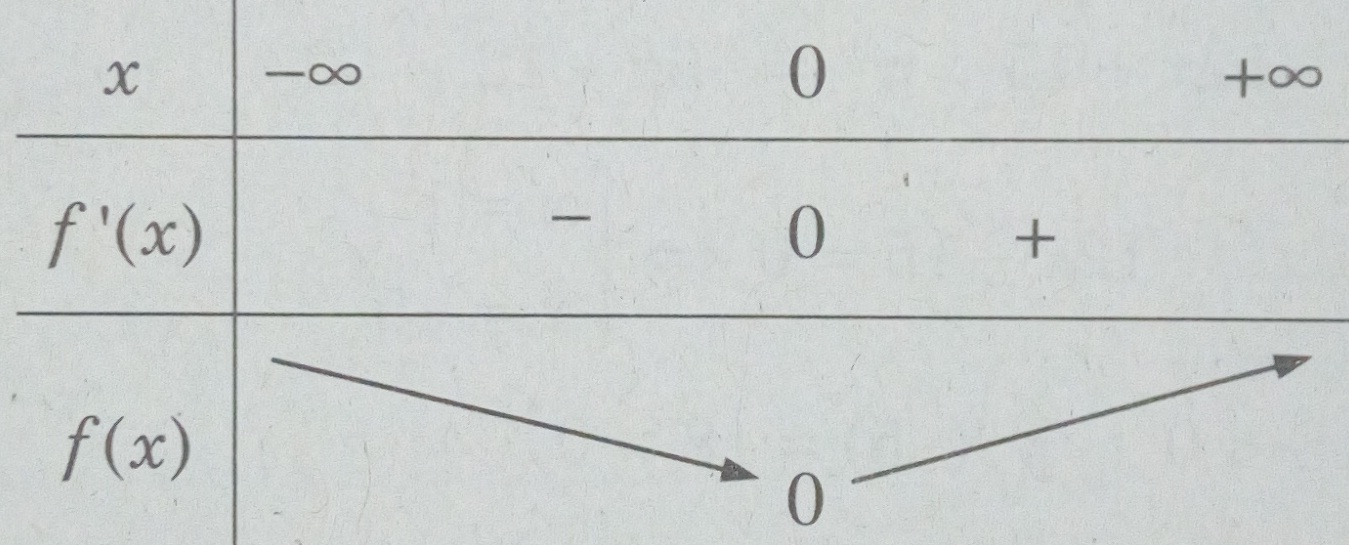
Hàm số \(f(x) = {e^x} + \cos x - 2 - x + {{{x^2}} \over 2} \ge {f_{CT}} = f(0) = 0,\forall x \in R\)

Từ đó suy ra điều phải chứng minh.

b) \(\forall x \ge 0\)  xét hàm số \(f(x) = {e^x} - {e^{ - x}} - 2\ln (x + \sqrt {1 + {x^2}} )\) , ta có

                \(f'(x) = {e^x} + {e^{ - x}} - {2 \over {\sqrt {1 + {x^2}} }}\)       ;

Từ đó f ‘(x) > 0 với mọi x > 0  (vì \({e^x} + {e^{ - x}} > 2\) và \({2 \over {\sqrt {1 + {x^2}} }} < 2\) ) và \(f ‘(x) = 0 \Leftrightarrow x = 0\)

Vậy f(x) đồng biến trên \({\rm{[}}0; + \infty )\) , tức là:

      \(f(x) \ge f(0) = {e^0} - {e^0} - 2\ln 1 = 0\)  

Từ đó suy ra điều cần chứng minh

c) Xét hàm số  \(f(x) = 8{\sin ^2}{x \over 2} + \sin 2x - 2x,\forall x \in (0;\pi {\rm{]}}\)

      \(f'(x) = 4\sin x + 2\cos 2x - 2 = 4\sin x(1 - \sin x)\)

\(f'(x) = 0 \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2}} \cr {x = \pi } \cr} } \right.\)           

Với  \(x \in (0;\pi {\rm{]}}\) ta có \(f'(x) \ge 0\)  và dấu bằng chỉ xảy ra tại hai điểm.

Vậy f(x) đồng biến trên nửa \((0;\pi {\rm{]}}\). Mặt khác, f(0) = 0 nên f(x) > 0.

Từ đó suy ra điều phải chứng minh.

Bài 5.8 trang 220 sách bài tập (SBT) - Giải tích 12

Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng:

a) g(x) = |x³ + 3x² – 72x + 90| trên đoạn [-5; 5]

b) f(x) = x⁴ – 4x² + 1 trên đoạn [-1; 2]

c) f(x) = x – ln x + 3 trên khoảng \((0; + \infty )\)

Hướng dẫn làm bài

a) Xét hàm số \(f(x) = {x^3} + 3{x^2} - 72x + 90\)  trên đoạn [-5; 5]

\(f'(x) = 3{x^2} + 6x - 72;f'(x) = 0\Leftrightarrow \left[ {\matrix{{x = 4} \cr {x = - 6 \notin {\rm{[}} - 5;5]} \cr} } \right.\)

\(f( - 5) = 400;f(5) =  - 70;f(4) =  - 86\)

Ngoài ra, f(x) liên tục trên đoạn [-5; 5] và \(f( - 5).f(5) < 0\) nên tồn tại \({x_0} \in ( - 5;5)\) sao cho \(f({x_0}) = 0\)

Ta có \(g(x) = |f(x)| \ge 0\) và \(g({x_0}) = |f({x_0})| = 0;g( - 5) = |400| = 400\);

 \(g(5) = |-70| = 70 ; g(4) = |f(4)| = |-86| = 86\)

Vậy \(\mathop {\min g(x)}\limits_{{\rm{[}} - 5;5]}  = g({x_0}) = 0;\mathop {{\rm{max }}g(x)}\limits_{{\rm{[}} - 5;5]}  = g( - 5) = 400\)

b)  \(\mathop {\min f(x)}\limits_{{\rm{[}} - 1;2]}  = f(\sqrt 2 ) =  - 3;\mathop {{\rm{max f}}(x)}\limits_{{\rm{[}} - 1;2]}  = f(2) = f(0) = 1\)

c) \(\mathop {\min f(x)}\limits_{(0; + \infty )}  = f(1) = 4\) . Không có giá trị lớn nhất.

Giaibaitap.me