Câu 4.4 trang 203 sách bài tập (SBT) - Giải tích 12
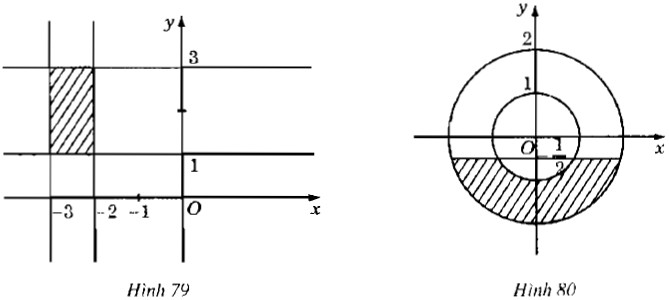
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình 87 và hình 88?
Hướng dẫn làm bài
a) Phần thực của z thuộc đoạn [-3; -2] trên trục Ox; phần ảo của z thuộc đoạn [1; 3] trên trục Oy.
b) Phần ảo của z nhỏ hơn hoặc bằng \( - {1 \over 2},1 \le |z| \le 2\).
Câu 4.5 trang 203 sách bài tập (SBT) - Giải tích 12
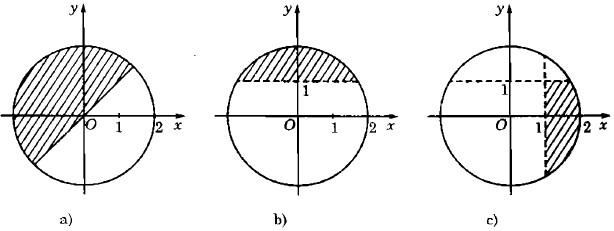
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| \( \le \) 2 và:
a) Phần thực của z không vượt quá phần ảo của nó;
b) Phần ảo của z lớn hơn 1;
c) Phần ảo của z nhỏ hơn 1, phần thực của z lớn hơn 1.
Hướng dẫn làm bài
Câu 4.6 trang 203 sách bài tập (SBT) - Giải tích 12
Tìm số phức z, biết:
a) |z| = 2 và z là số thuần ảo;
b) |z| = 5 và phần thực của z bằng hai lần phần ảo của nó;
c) \(z = \bar z\)
d) \(z = - \bar z\)
Hướng dẫn làm bài
a) \(z = \pm 2i\)
b) \(z = \pm (2\sqrt 5 + i\sqrt 5 )\)
c) z là một số thực \(\overline {({{{z_1}} \over {{z_2}}})} = {{{{\bar z}_1}} \over {{{\bar z}_2}}}\)
d) z là một số thuần ảo.
Câu 4.7 trang 203 sách bài tập (SBT) - Giải tích 12
Có thể nói gì về các điểm biểu diễn hai số phức z1 và z2, biết:
a) |z1| = |z2| ? b)\({z_1} = {\bar z_2}\) ?
Hướng dẫn làm bài
a) Các điểm biểu diễn z1 và z2 cùng nằm trên đường tròn có tâm là gốc tọa độ O.
b) Các điểm biểu diễn z1 và z2 đối xứng với nhau qua trục Ox.
Giaibaitap.me
Giải bài tập trang 206 bài 2 phép cộng và phép nhân các số phức Sách bài tập (SBT) Giải tích 12. Câu 4.15: Thực hiện các phép tính...
Giải bài tập trang 205 bài 2 phép cộng và phép nhân các số phức Sách bài tập (SBT) Giải tích 12. Câu 4.8: Thực hiện các phép tính...
Giải bài tập trang 205, 206 bài 2 phép cộng và phép nhân các số phức Sách bài tập (SBT) Giải tích 12. Câu 4.12: Cho x, y là những số phức. Chứng minh rằng mỗi cặp số sau là hai số phức liên hợp với nhau...
Giải bài tập trang 207 bài 3 phép chia số phức Sách bài tập (SBT) Giải tích 12. Câu 4.18: Thực hiện các phép tính sau...
