Bài 1.14 trang 20 sách bài tập (SBT) – Hình học 12

Cho hình hộp chữ nhật ABCD.A’B’C’D’  có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD.

a) Tính thể tích khối chóp M.AB’C

b) Tính khoảng cách từ M đến mặt phẳng (AB’C).

Hướng dẫn làm bài:

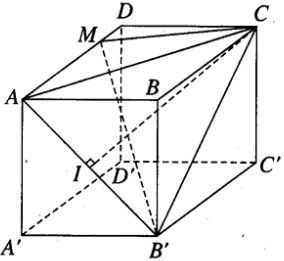
a) Thể tích khối chóp M.AB’C bằng thể tích khối chóp B’AMC. Ta có:

\({S_{AMC}} = {3 \over 4}{S_{ADC}} = {3 \over 4}.{1 \over 2}.2{a^2} = {{3{a^2}} \over 4}\)

Do đó  \({V_{M.AB'C}} = {1 \over 3}.{{3{a^2}} \over 4}.a = {{{a^3}} \over 4}\)

b) Gọi h là khoảng cách từ M đến mặt phẳng (AB’C)

Khi đó  \({V_{M.AB'C}} = {1 \over 3}{S_{AB'C}}.h = {{{a^3}} \over 4}\)

Vì   AC² = B’C² = 5a²  nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao.

Ta có:  \(C{I^2} = {\rm{ }}C{A^2}-{\rm{ }}A{I^2} = {\rm{ }}5{a^2} - {({{a\sqrt 2 } \over 2})^2} = 5{a^2} - {{{a^2}} \over 2} = {{9{a^2}} \over 2}\)

Do đó  \(CI = {{3a} \over {\sqrt 2 }}\Rightarrow {S_{AB'C}} = {1 \over 2}.{{3a} \over {\sqrt 2 }}.a\sqrt 2  = {{3{a^2}} \over 2}\)

Từ đó suy ra \(h = 3{{{a^3}} \over 4}:{{3{a^2}} \over 2} = {a \over 2}\)

Bài 1.15 trang 21 sách bài tập (SBT) – Hình học 12

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’.  Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’

Hướng dẫn làm bài

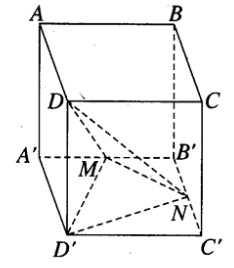
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN

Ta có:  \({S_{D'MN}} = {S_{A'B'C'D'}} - ({S_{D'A'M}} + {S_{D'C'N}} + {S_{B'MN}})\)

\(= ab - ({{ab} \over 4} + {{ab} \over 8} + {{ab} \over 4}) = {{3ab} \over 8}\)

Thể tích khối chóp  \({V_{D'.DMN}} = {1 \over 3}.{{3ab} \over 8}.c = {{abc} \over 8}\)

Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng \({1 \over 8}\) . 

Bài 1.16 trang 21 sách bài tập (SBT) – Hình học 12

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho \(BE = {1 \over 2}EB',DF = {1 \over 2}FD'\) . Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).

Hướng dẫn làm bài:

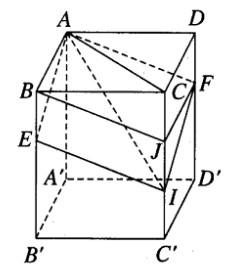
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.

Từ đó suy ra  \({\rm{IJ}} = EB = DF = JC = {c \over 3}\)

Ta có  \({S_{BCIE}} = {1 \over 2}({{c + 2c} \over 3})b = {{bc} \over 2}\)

       \({S_{DCIF}} = {1 \over 2}({{c + 2c} \over 3})a = {{ac} \over 2}\)    

Nên \({V_{(H)}} = {V_{A.BCIE}} + {V_{A.DCIF}} = {1 \over 3}.{{bc} \over 2}.a + {1 \over 3}.{{ac} \over 2}.b = {{abc} \over 3}\)

Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên \({V_{(H')}} = {2 \over 3}abc\)

Từ đó suy ra  \({{{V_{(H)}}} \over {{V_{(H')}}}} = {1 \over 2}\)

Bài 1.17 trang 21 sách bài tập (SBT) – Hình học 12

Cho hình hộp ABCD.A’B’C’D’ . Gọi E và F lần lượt là trung điểm của B’C’ và C’D’ . Mặt phẳng (AEF) chia hình hộp đó thành hai hình đa diện (H) và (H’), trong đó (H) là hình đa diện chứa đỉnh A’. Tính tỉ số giữa thể tích hình đa diện (H) và thể tích hình đa diện (H’).

Hướng dẫn làm bài:

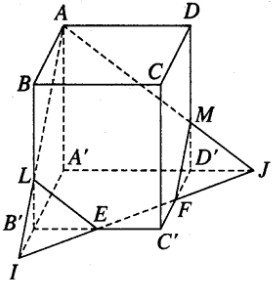
Giả sử đường thẳng EF cắt đường thẳng A’B’ tại I và cắt đường thẳng A’D’ tại J. AI cắt BB’ tại L, AJ cắt DD’ tại M. Gọi V₀ là thể tích khối tứ diện AA’IJ.  V là thể tích khối hộp ABCD.A’B’C’D’

Vì EB’ = EC’ và B’I // C’F  nên \(IB' = FC' = {{A'B'} \over 2}\)

Do đó  \({{IB'} \over {IA'}} = {1 \over 3}\)

Để ý rằng  BE’ // A’J  , B’L //AA’

Ta có  \({{IL} \over {IA}} = {{IE} \over {{\rm{IJ}}}} = {{IB'} \over {IA'}} = {1 \over 3}\)

Từ đó suy ra:  \({{{V_{I.ELB'}}} \over {{V_{I.JAA'}}}} = {({1 \over 3})^3} = {1 \over {27}}\)

Do đó  \({V_{I.ELB'}} = {1 \over {27}}{V_0}\)

Tương tự  \({V_{J.MFD'}} = {1 \over {27}}{V_0}\)

Gọi AB = a, BC = b , đường cao hạ từ A xuống (A’B’C’D’) là h thì

\(V = {V_{ABCD.A'B'C'D'}} = hab.\sin \widehat {BAD}\),

\({V_0} = {1 \over 3}({1 \over 2}.{{3a} \over 2}.{{3b} \over 2}\sin \widehat {BAD})h = {{3V} \over 8}\)

Vậy  \({V_{(H)}} = {V_0} - {2 \over {27}}{V_0} = {{25} \over {27}}{V_0} = {{25} \over {27}}.{{3V} \over 8} = {{25} \over {72}}V,{V_{(H')}} = {{47} \over {72}}V\),

\({V_{(H')}} = {{47} \over {72}}V,{{{V_{(H)}}} \over {{V_{(H')}}}} = {{25} \over {47}}\)

Giaibaitap.me