Bài 4.27 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?

A. \(\overrightarrow u  = (2;3)\) và \(\overrightarrow v  = \left( {\frac{1}{2};6} \right)\)

B. \(\overrightarrow a  = (\sqrt 2 ;6)\) và \(\overrightarrow b  = (1;3\sqrt 2 )\)

C. \(\overrightarrow i  = (0;1)\) và \(\overrightarrow j  = (1;0)\)

D. \(\overrightarrow c  = (1;3)\) và \(\overrightarrow d  = (2; - 6)\)

Phương pháp:

Cho \(\overrightarrow a  = (x;y)\) và \(\overrightarrow b  = (z,t)\) (\(z,t \ne 0\))

+) Nếu \(\frac{x}{z} = \frac{y}{t} = k\) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương

+) Nếu \(\frac{x}{z} \ne \frac{y}{t}\) thì \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương.

Lời giải:

Bài 4.28 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?

A. \(\overrightarrow u  = (2;3)\) và \(\overrightarrow v  = \left( {4;6} \right)\)

B. \(\overrightarrow a  = (1; - 1)\) và \(\overrightarrow b  = ( - 1;1)\)

C. \(\overrightarrow z  = (a;b)\) và \(\overrightarrow t  = ( - b;a)\)

D. \(\overrightarrow n  = (1;1)\) và \(\overrightarrow k  = (2;0)\)

Phương pháp:

+) Cho \(\overrightarrow u \;(x;y),\;\overrightarrow v \;(z;t)\) thì \(\overrightarrow u .\overrightarrow v  = x.z + y.t\)

+) \(\overrightarrow u\; \bot\overrightarrow v\Leftrightarrow \overrightarrow u .\;\overrightarrow v = 0\)

Lời giải:

Ta có: \(\overrightarrow u .\overrightarrow v  = 2.4 + 3.6 = 26 \ne 0\). Suy ra hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) không vuông góc với nhau. Do đó A sai.

Ta có: \(\overrightarrow a .\overrightarrow b  = 1.( - 1) + ( - 1).1 =  - 2 \ne 0\). Suy ra hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) không vuông góc với nhau. Do đó B sai.

Ta có: \(\overrightarrow z .\overrightarrow t  = a.( - b) + b.a = 0\). Suy ra hai vecto \(\overrightarrow z \) và \(\overrightarrow t \) vuông góc với nhau. Do đó C đúng.

Ta có: \(\overrightarrow n .\overrightarrow k  = 1.2 + 1.0 = 2 \ne 0\). Suy ra hai vecto \(\overrightarrow n \) và \(\overrightarrow k \) không vuông góc với nhau. Do đó D sai.

Chọn C.

Bài 4.29 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?

A. \(\overrightarrow a  = (1;1)\)

B. \(\overrightarrow b  = (1; - 1)\)

C. \(\overrightarrow c  = \left( {2;\frac{1}{2}} \right)\)

D. \(\overrightarrow d  = \left( {\dfrac{1}{{\sqrt 2 }};\dfrac{{ - 1}}{{\sqrt 2 }}} \right)\)

Phương pháp:

Tính độ dài vectơ \(\overrightarrow a \;(x;y)\) theo công thức: \(|\overrightarrow a |\, = \sqrt {{x^2} + {y^2}} \).

Lời giải:

Vì \(\overrightarrow a  = (1;1) \Rightarrow \;|\overrightarrow a |\; = \sqrt {{1^2} + {1^2}}  = \sqrt 2  \ne 1\). Do đó A sai.

Vì \(\overrightarrow b  = (1; - 1) \Rightarrow \;|\overrightarrow b |\; = \sqrt {{1^2} + {{( - 1)}^2}}  = \sqrt 2  \ne 1\).Do đó B sai.

Vì \(\overrightarrow c  = \left( {2;\dfrac{1}{2}} \right) \Rightarrow \;|\overrightarrow c |\; = \sqrt {{2^2} + {{\left( {\dfrac{1}{2}} \right)}^2}}  = \dfrac{{\sqrt {17} }}{2} \ne 1\). Do đó C sai.

Vì Ta có: \(\overrightarrow d  = \left( {\dfrac{1}{{\sqrt 2 }};\frac{{ - 1}}{{\sqrt 2 }}} \right) \Rightarrow \;|\overrightarrow a |\; = \sqrt {{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2} + {{\left( {\frac{{11}}{{\sqrt 2 }}} \right)}^2}}  = 1\). Do đó D đúng.

Chọn D

Bài 4.30 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Góc giữa vectơ \(\overrightarrow a  = \left( {1; - 1} \right)\) và vectơ \(\overrightarrow b  = ( - 2;0)\) có số đo bằng:

A. \({90^o}\)

B. \({0^o}\)

C. \({135^o}\)

D. \({45^o}\)

Lời giải: 

Ta có: \(\overrightarrow a .\overrightarrow b  = 1.( - 2) + ( - 1).0 =  - 2 \ne 0\),

\(|\overrightarrow a | = \sqrt {{1^2} + {{( - 1)}^2}}  = \sqrt 2 ;\;|\overrightarrow b | = \sqrt {{{( - 2)}^2} + {0^2}}  = 2.\)

\( \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.\;|\overrightarrow b |}} = \frac{{ - 2}}{{\sqrt 2 .2}} = \frac{{ - \sqrt 2 }}{2}\)

\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {135^o}\)

Chọn C

Bài 4.31 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Khẳng định nào sau đây là đúng?

A. \(( {\overrightarrow a .\overrightarrow b } )\overrightarrow c  = \overrightarrow a \,\,( {\overrightarrow b .\overrightarrow c })\)

B. \({( {\overrightarrow a .\overrightarrow b })^2} = {\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}\)

C. \(\overrightarrow a .\overrightarrow b  = | {\overrightarrow a } |.\left| {\overrightarrow b } \right|\,\sin ( {\overrightarrow a ,\overrightarrow b } )\)

D. \(\overrightarrow a \,\,( {\overrightarrow b  - \overrightarrow c }) = \overrightarrow a .\overrightarrow b  - \overrightarrow a .\,\overrightarrow c \)

Lời giải: 

Theo tính chất của tích vô hướng ta có: \(\overrightarrow a \,\,( {\overrightarrow b  - \overrightarrow c }) = \overrightarrow a .\overrightarrow b  - \overrightarrow a .\,\overrightarrow c \) (tính chất phân phối đối với phép trừ)

Chọn D 

Bài 4.32 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?

A. \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^o}\)

B. \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^o}\) và \(\overrightarrow {AC} .\overrightarrow {BC}  = {a^2}\)

C. \(\overrightarrow {AC} .\overrightarrow {BD}  = {a^2}\sqrt 2 \)

D. \(\overrightarrow {BA} .\overrightarrow {BD}  =  - {a^2}\)

Lời giải:

Lấy các điểm E, F sao cho ABDE, ABFC là các hình bình hành.

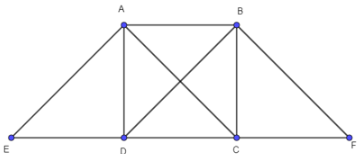
Chọn B.

Bài 4.33 trang 71 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3 MC.

a) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \)

b) Biểu thị vectơ \(\overrightarrow {AM} \) theo hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).

Lời giải:

a) Hai vecto \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) là hai vecto ngược hướng và MB = 3MC nên ta có:\(\overrightarrow {MB} = -3.\overrightarrow {MC}\) 

Vậy mối liên hệ là: \(\overrightarrow {MB} = -3.\overrightarrow {MC}\) 

b) 

Ta có: \(\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM} \)

\( \overrightarrow {AM}  = \overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {BC} \)

\( \overrightarrow {AM}  = \overrightarrow {AB}  + \dfrac{3}{4}\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)= \dfrac{1}{4}.\overrightarrow {AB}  + \dfrac{3}{4}.\overrightarrow {AC} \)

Vậy \(\overrightarrow {AM}  = \dfrac{1}{4}.\overrightarrow {AB}  + \dfrac{3}{4}.\overrightarrow {AC} \)

Bài 4.34 trang 72 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

\(\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MB}  + \overrightarrow {MD} \).

Phương pháp:

+) ABCD là hình bình hành thì: \(\overrightarrow {AB}  = \overrightarrow {DC} \)

Lời giải:

Do ABCD là hình bình hành nên \(\overrightarrow {AB}  = \overrightarrow {DC} \)

\(\begin{array}{l} \Rightarrow \overrightarrow {AM}  + \overrightarrow {MB}  = \overrightarrow {DM}  + \overrightarrow {MC} \\ \Leftrightarrow  - \overrightarrow {MA}  + \overrightarrow {MB}  =  - \overrightarrow {MD}  + \overrightarrow {MC} \\ \Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MB}  + \overrightarrow {MD} \end{array}\)

Bài 4.35 trang 72 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Trong mặt phẳng tọa độ Oxy, cho A (2; 1), B (-2; 5) và C (-5; 2).

a) Tìm tọa độ của các vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \)

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Lời giải:

a) Ta có:  \(\overrightarrow {BA} = (4; - 4)\) và \(\overrightarrow {BC} = ( - 3; - 3)\).

b) Ta có: \(\overrightarrow {BA} .\overrightarrow {BC}  = 4.( - 3) + ( - 4).( - 3) = 0\) 

\( \Rightarrow \overrightarrow {BA}  \bot \overrightarrow {BC} \) hay \(\widehat {ABC} = {90^o}\) 

Vậy tam giác ABC vuông tại B. 

Diện tích tam giác vuông ABC là: \(AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{4^2} + {{( - 4)}^2}}  = 4\sqrt 2 \); \(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{3^2} + {{( - 3)}^2}}  = 3\sqrt 2 \) 

Và \(AC = \sqrt {A{B^2} + B{C^2}}  = 5\sqrt 2 \) (do \(\Delta ABC\)vuông tại B). 

Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}.4\sqrt 2 .3\sqrt 2  = 12\) 

Chu vi tam giác ABC là: \(AB + BC + AC = 4\sqrt 2  + 3\sqrt 2  + 5\sqrt 2  = 12\sqrt 2 \)

c) Tọa độ của trọng tâm G là \(\left( {\frac{{2 + ( - 2) + ( - 5)}}{3};\frac{{1 + 5 + 2}}{3}} \right) = \left( {\frac{{ - 5}}{3};\frac{8}{3}} \right)\)

d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).

Ta có: \(\overrightarrow {BC}  = ( - 3; - 3)\) và \(\overrightarrow {AD}  = (a - 2;b - 1)\)

Vì BCAD là một hình bình hành  nên \(\overrightarrow {AD}  = \overrightarrow {BC} \)

\(\begin{array}{l} \Leftrightarrow (a - 2;b - 1) = ( - 3; - 3)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 2 =  - 3\\b - 1 =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b =  - 2\end{array} \right.\end{array}\)

Vậy D có tọa độ (-1; -2) 

Bài 4.36 trang 72 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức: 

Trong mặt phẳng tọa độ Oxy, cho A (1; 2), B (3; 4), C (-1; -2) và D (6;5).

a) Hãy tìm tọa độ của các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) 

b) Hãy giải thích tại sao các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng phương. 

c) Giả sử E là điểm có tọa độ (a; 1). Tìm a để các vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BE} \) cùng phương. 

d) Với a tìm được, hãy biểu thị vectơ \(\overrightarrow {AE} \) theo các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).

Lời giải:

a) Ta có:  \(\overrightarrow {AB} = (2;2)\) và \(\overrightarrow {CD} = (7;7)\)

b) Ta có: \((2;2) = \frac{2}{7}.(7;7)\)\( \Rightarrow \overrightarrow {AB}  = \frac{2}{7}.\overrightarrow {CD} \)

Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng phương.

c) Ta có: \(\overrightarrow {AC} = ( - 2; - 4)\) và \(\overrightarrow {BE} = (a - 3; - 3)\)

Để \(\overrightarrow {AC} \) và \(\overrightarrow {BE} \) cùng phương thì \(\frac{{a - 3}}{{ - 2}} = \frac{{ - 3}}{{ - 4}}\)\( \Leftrightarrow a - 3 =  - \frac{3}{2}\)\( \Leftrightarrow a = \frac{3}{2}\)

Vậy \(a = \frac{3}{2}\) hay \(E\left( {\frac{3}{2};1} \right)\) thì hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BE} \) cùng phương.

d) Ta có: \(\overrightarrow {BE}  = \left( {\frac{3}{2} - 3; - 3} \right) = \left( { - \frac{3}{2}; - 3} \right)\) ; \(\overrightarrow {AC}  = ( - 2; - 4)\)

\( \Rightarrow \overrightarrow {BE}  = \frac{3}{4}.\overrightarrow {AC} \)

Mà \(\overrightarrow {AE}  = \overrightarrow {AB}  + \overrightarrow {BE} \) (quy tắc cộng)

\( \Rightarrow \overrightarrow {AE}  = \overrightarrow {AB}  + \frac{3}{4}.\overrightarrow {AC} \)

Bài 4.37 trang 72 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Cho vectơ \(\overrightarrow a  \ne \overrightarrow 0 \). Chứng minh rằng \(\frac{1}{{|\overrightarrow a |}}\;\overrightarrow a \) (hay còn được viết là \(\frac{{\overrightarrow a }}{{|\overrightarrow a |}}\)) là một vectơ đơn vị, cùng hướng với vectơ \(\overrightarrow a \).

Phương pháp: 

Lời giải:  

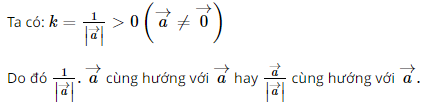
Bài 4.38 trang 72 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Cho ba vectơ \(\overrightarrow a ,\;\overrightarrow b ,\;\overrightarrow u \) với \(|\overrightarrow a |\; = \;\,|\overrightarrow b |\; = 1\) và \(\overrightarrow a  \bot \overrightarrow b \). Xét một hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i  = \overrightarrow a ,\;\overrightarrow j  = \overrightarrow b .\) Chứng minh rằng: 

a) Vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\) 

b) \(\overrightarrow u  = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a  + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \)

Phương pháp:

a) Trên hệ trục Oxy mới, xác định hoành độ, tung độ của vectơ \(\overrightarrow u \)

+) \(\overrightarrow u \,.\,\overrightarrow a = |\overrightarrow u| \,.\,|\overrightarrow a|. \cos (\overrightarrow u \,.\,\overrightarrow a) \)

b) Vectơ \(\overrightarrow u \) có tọa độ \((x\,;y)\) trong hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i ;\;\overrightarrow j \) thì \(\overrightarrow u  = x\,.\,\overrightarrow i  + y.\,\overrightarrow j \)

Lời giải:

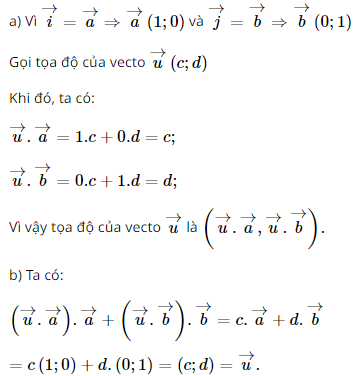
Bài 4.39 trang 72 SGK Toán lớp 10 tập 1 - Kết Nối Tri Thức:

Trên sông, một cano chuyển động thẳng đều theo hướng \(S{15^o}E\) với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.

Phương pháp:

Định lí cosin trong tam giác OAC: \(A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\)

Lời giải:

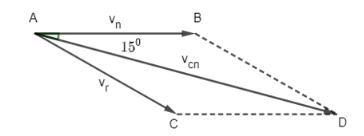
= 3² + 20² – 2.3.20.cos15⁰

≈ 291,09

⇒ v_r ≈ 17,12

Vậy vận tốc riêng của ca nô là 17,12 km/h.

Giaibaitap.me