Câu 71 trang 61 Sách bài tập (SBT) Toán 8 tập 2
Cho các bất đẳng thức
\(a > b;a < b;c > 0;c < 0;a + c < b + c;a + c > b + c;ac < bc;ac > bc\)
Hãy đặt các bất đẳng thức thích hợp vào chỗ trống (…) trong câu sau:
|
Nếu ……………………, và ……………………… thì ……………………...... |
Giải:
Nếu a > b và c > 0 thì ac > bc
Nếu a > b và c > 0 thì a + c > b + c
Nếu a > b và c < 0 thì a + c > b + c
Nếu a > b và c < 0 thì ac < bc
Nếu a < b và c > 0 thì ac < bc
Nếu a < b và c > 0 thì a + c < b + c
Nếu a < b và c < 0 thì ac > bc
Nếu a < b và c < 0 thì a + c < b + c
Câu 72 trang 61 Sách bài tập (SBT) Toán 8 tập 2
Cho a > b, chứng tỏ
a. \(3a + 5 > 3b + 2\)
b. \(2 - 4a < 3 - 4b\)
Giải:
a. Ta có: \(a > b \Leftrightarrow 3a > 3b \Leftrightarrow 3a + 5 > 3b + 5\) (1)
Mặt khác: 3b + 5 > 3b + 2 (2)
Từ (1) và (2) suy ra: 3a + 5 > 3b + 2
b. Ta có: \(a > b \Leftrightarrow - 4a < - 4b \Leftrightarrow 3 - 4a < 3 - 4b\) (1)
Mặt khác: \(2 - 4a < 3 - 4a\) (2)
Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b
Câu 73 trang 61 Sách bài tập (SBT) Toán 8 tập 2
a. Chứng tỏ 2,99 là nghiệm của bất phương trình 3 > x. Hãy kể ra ba số lớn hơn 2,99 mà cũng là nghiệm của bất phương trình đó.
b. Chứng tỏ 4,01 là nghiệm của bất phương trình 4 < x. Hãy kể ra ba số nhỏ hơn 4,01 mà cũng là nghiệm của bất phương trình đó.
Giải:
a. Ta có 2,99 là nghiệm của bất phương trình x < 3. Bốn số lớn hơn 2,99 là nghiệm của bất phương trình là: 2,999; 2,998; 2,997; 2,996.
b. Ta có 4,01 là nghiệm của bất phương trình x > 4. Ba số nhỏ hơn 4,01 là nghiệm của bất phương trình là: 4,003; 4,002; 4,001.
Câu 74 trang 61 Sách bài tập (SBT) Toán 8 tập 2
Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số:
a. \(2\left( {3x - 1} \right) - 2x < 2x + 1\)
b. \(4x - 8 \ge 3\left( {3x - 2} \right) + 4 - 2x\)
Giải:
a. Ta có:
\(\eqalign{ & 2\left( {3x - 1} \right) - 2x < 2x + 1 \cr & \Leftrightarrow 6x - 2 - 2x < 2x + 1 \cr & \Leftrightarrow 6x - 2x - 2x < 1 + 2 \cr & \Leftrightarrow 2x < 3 \Leftrightarrow x < {3 \over 2} \cr} \)
Vậy tập nghiệm của bất phương trình là: \(\left\{ {x|x < {3 \over 2}} \right\}\)
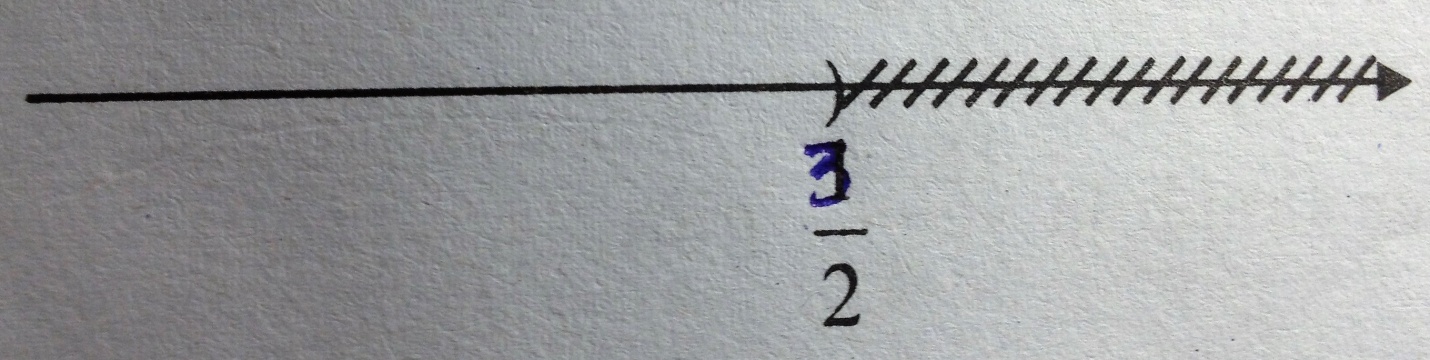
b. Ta có:
\(\eqalign{ & 4x - 8 \ge 3\left( {3x - 2} \right) + 4 - 2x \cr & \Leftrightarrow 4x - 8 \ge 9x - 6 + 4 - 2x \cr & \Leftrightarrow 4x - 9x + 2x \ge - 6 + 4 + 8 \cr & \Leftrightarrow - 3x \ge 6 \Leftrightarrow x \le - 2 \cr} \)
Vậy tập nghiệm của bất phương trình là: \(\left\{ {x|x \le - 2} \right\}\)
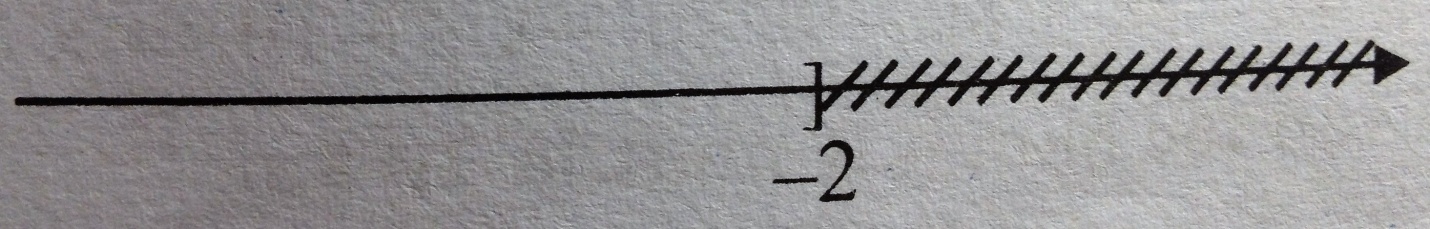
Giaibaitap.me
Giải bài tập trang 61, 62 bài ôn tập chương IV - Bất phương trình bậc nhất một ẩn Sách bài tập (SBT) Toán 8 tập 2. Câu 75: Giải các bất phương trình...
Giải bài tập trang 61, 62 bài ôn tập chương IV - Bất phương trình bậc nhất một ẩn Sách bài tập (SBT) Toán 8 tập 2. Câu 79: Với số m và số n bất kì, chứng tỏ rằng...
Giải bài tập trang 62 bài ôn tập chương IV - Bất phương trình bậc nhất một ẩn Sách bài tập (SBT) Toán 8 tập 2. Câu 83: Giải phương trình...
Giải bài tập trang 62 bài ôn tập chương IV - Bất phương trình bậc nhất một ẩn Sách bài tập (SBT) Toán 8 tập 2. Câu 87: Với giá trị nào của x thì...
