Câu 44 trang 95 Sách bài tập (SBT) Toán 8 tập 2

Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M (h.30). Tính độ dài của đoạn thẳng CD.

Giải:

(hình 30 trang 95 sbt)

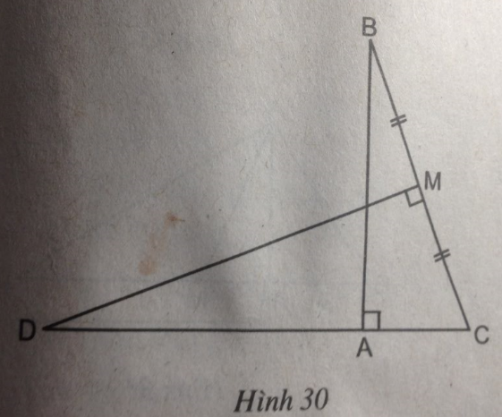
Xét hai tam giác vuông ABC và MDC, ta có:

\(\widehat {BAC} = \widehat {DMC} = 90^\circ \)

 chung

Suy ra: tam giác ABC đồng dạng tam giác MDC (g.g)

Suy ra: \({{AC} \over {MC}} = {{BC} \over {DC}}\)

Suy ra: \(DC = {{MC.BC} \over {AC}}\)

Ta có: \(MC = {1 \over 2}BC = {1 \over 2}.24 = 12\)  (cm)

Vậy DC = \({{12.24} \over 9} = 32\)  (cm)

Câu 45 trang 95 Sách bài tập (SBT) Toán 8 tập 2

Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn thẳng AE = 8cm (h.31). Chứng minh góc BEC = 90°

Giải:

(hình 31 trang 95 sbt)

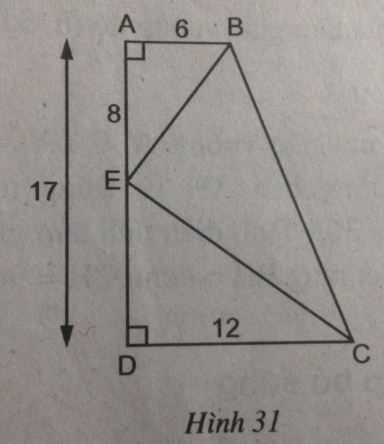
Ta có: AD = AE + DE

Suy ra: DE = AD – AE

=17 – 8 = 9 (cm)

Xét ∆ ABE và ∆ DEC, ta có:

\(\widehat A = \widehat D = 90^\circ \)   (1)

Mà \({{AB} \over {DE}} = {6 \over 9} = {2 \over 3}\)

\({{AE} \over {DC}} = {8 \over {12}} = {2 \over 3}\)

Suy ra: \({{AB} \over {DE}} = {{AE} \over {DC}}\)          (2)

Từ (1) và (2) suy ra ∆ DEC đồng dạng ∆ ABE (c.g.c)

Suy ra: \(\widehat {AEB} = \widehat {DEC}\)

Trong ∆ ABE ta có: \(\widehat A = 90^\circ  \Rightarrow \widehat {ABE} + \widehat {AEB} = 90^\circ \)

Suy ra: \(\widehat {DEC} + \widehat {AEB} = 90^\circ \)

Lại có: \(\widehat {ABE} + \widehat {BEC} + \widehat {DEC} = \widehat {AED} = 180^\circ \)  (kề bù)

Vậy \(\widehat {BEC} = 180^\circ  - \left( {\widehat {AEB} + \widehat {DEC}} \right) = 180^\circ  - 90^\circ  = 90^\circ \)

Câu 46 trang 95 Sách bài tập (SBT) Toán 8 tập 2

Cho tam giác ABC vuông tại A, AC = 4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC).Lấy trên tia Cx điểm D sao cho BD = 9cm (h.32)

Chứng minh rằng BD // AC.

Giải:

(hình 32 trang 95 sbt)

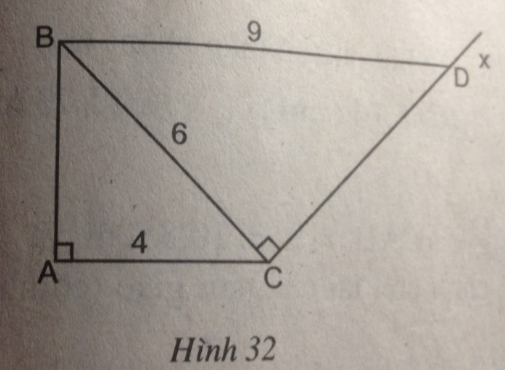
Xét hai tam giác vuông ABC và CDB, ta có:

\(\widehat {BAC} = \widehat {DCB} = 90^\circ \)    (1)

Mà \({{AC} \over {CB}} = {4 \over 6} = {2 \over 3}\)

\({{CB} \over {BD}} = {6 \over 9} = {2 \over 3}\)

Suy ra: \({{AC} \over {CB}} = {{CB} \over {BD}}\)     (2)

Từ (1) và (2) suy ra ∆ ABC đồng dạng ∆ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)

Suy ra: \(\widehat {ACB} = \widehat {CBD}\)

Vậy AC // BD (vì có các cặp góc ở vị trí so le trong bằng nhau).

Câu 47 trang 95 Sách bài tập (SBT) Toán 8 tập 2

Trên hình 33 hãy chỉ ra các tam giác đồng dạng. Viết các cặp tam giác đồng dạng  theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng.

Giải:

(hình 33 trang 95 sbt)

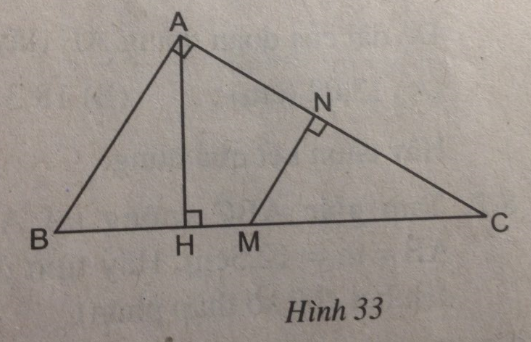
- ∆ ABC đồng dạng ∆ HBA

Hai tam giác vuông có góc nhọn ở đỉnh B chung.

- ∆ ABC đồng dạng ∆ HAC

Hai tam giác vuông có góc nhọn ở đỉnh C chung.

- ∆ ABC đồng dạng ∆ NMC

Hai tam giác vuông có góc nhọn ở đỉnh C chung.

- ∆ HAC đồng dạng ∆ NMC

Hai tam giác vuông có góc nhọn ở đỉnh C chung.

- ∆ HAC đồng dạng ∆ HBA

Hai tam giác vuông có góc nhọn \(\widehat {HBA} = \widehat {HAC}\)

- ∆ HAB đồng dạng ∆ NCM

Hai tam giác vuông có góc nhọn \(\widehat {HAB} = \widehat {NCM}\)

Giaibaitap.me