Câu 6 trang 84 Sách bài tập (SBT) Toán 8 tập 2
Cho tam giác ABC có cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N (h.5)
Tính theo a độ dài của các đoạn thẳng DM và EN.
Giải:

Ta có: AD = DE = EB = \({1 \over 3}AB\) (1)
Suy ra: AE = AD + DE = \({2 \over 3}AB\) (2)
Trong ∆ ABC, ta có : DM // BC (gt)
Nên \({{AD} \over {AB}} = {{DM} \over {BC}}\) (hệ quả định lí Ta-lét)
Suy ra: \({{AD} \over {AB}} = {{DM} \over a}\) (3)
Từ (1) và (3) suy ra: \({{DM} \over a} = {1 \over 3}\)
Suy ra: \(DM = {1 \over 3}a\)
Trong ∆ABC, ta có: EN // BC (gt)
Suy ra: \({{AE} \over {AB}} = {{EN} \over {BC}}\) (hệ quả định lí Ta-lét)
Suy ra: \({{AE} \over {AB}} = {{EN} \over a}\) (4)
Từ (2) và (4) suy ra: \({{EN} \over a} = {2 \over 3}\) hay \(EN = {2 \over 3}a\)
Câu 7 trang 84 Sách bài tập (SBT) Toán 8 tập 2
Hình 6 chi biết MN // BC, AB = 25cm, BC = 45cm, AM = 16cm, AN = 10cm.
Tính độ dài x, y của các đoạn thẳng MN, AC.
Giải:
(xem hình 6)
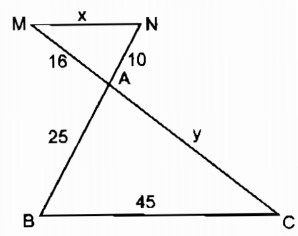
Trong ∆ ABC, ta có: MN // BC (gt)
Suy ra: \({{AN} \over {AB}} = {{AM} \over {AC}} = {{MN} \over {BC}}\) (hệ quả định lí Ta-lét)
Suy ra: \({{10} \over {25}} = {{16} \over y} = {x \over {45}}\)
Vậy : \(y = {{25.16} \over {10}} = 40\)
\(x = {{10.45} \over {25}} = 18\)
Câu 8 trang 84 Sách bài tập (SBT) Toán 8 tập 2
Hình 7 cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC và BC.
Giải:
(xem hình 7)
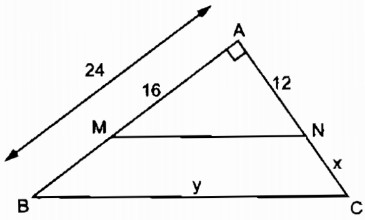
Trong ∆ ABC ta có: MN // BC (gt)
Suy ra: \({{AM} \over {AB}} = {{AN} \over {AC}}\) (định lí Ta-lét)
Suy ra: \(AC = {{AB.AN} \over {AM}} = {{24.12} \over {16}} = 18\) (cm)
Vậy: NC = AC – AN = 18 – 12 = 6 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
\(\eqalign{ & M{N^2} = A{M^2} + A{N^2} = {16^2} + {12^2} = 400 \cr & MN = 20(cm) \cr} \)
Trong ∆ABC, ta có: MN // BC (gt)
Suy ra: \({{AM} \over {AB}} = {{MN} \over {BC}}\) (hệ quả định lí Ta-lét)
Vậy: \(BC = {{MN.AB} \over {AM}} = {{20.24} \over {16}} = 30\) (cm)
Câu 9 trang 84 Sách bài tập (SBT) Toán 8 tập 2
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O (h.8).
Chứng minh rằng: OA.OD = OB.OC.
Giải:
(hình 8 trang 84 sbt)
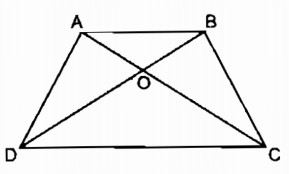
Trong ∆ OCD, ta có: AB // CD (gt)
Suy ra: \({{OA} \over {OC}} = {{OB} \over {OD}}\) (hệ quả định lí Ta-lét)
Vậy OA.OD = OB.OC.
Giaibaitap.me
Giải bài tập trang 84, 85 bài 2 định lí đảo và hệ quả của định lí Ta-lét Sách bài tập (SBT) Toán 8 tập 2. Câu 10: Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q...
Giải bài tập trang 85, 86 bài 2 định lí đảo và hệ quả của định lí Ta-lét Sách bài tập (SBT) Toán 8 tập 2. Câu 14: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O...
Giải bài tập trang 86 bài 2 định lí đảo và hệ quả của định lí Ta-lét Sách bài tập (SBT) Toán 8 tập 2. Câu 2.1: Hình bs.1 cho biết AB // CD, O ∈ MN, MN = 5cm, OB = 1,5cm, OD = 4,5cm, MB = 1cm....
Giải bài tập trang 87 bài 3 tính chất đường phân giác của tam giác Sách bài tập (SBT) Toán 8 tập 2. Câu 17: Tính độ dài đoạn thẳng DB và DC...
