Câu 17 trang 87 Sách bài tập (SBT) Toán 8 tập 2

Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt BC tại D (h.14)

a. Tính độ dài đoạn thẳng DB và DC

b. Tính tỉ số diện tích của hai tam giác ABD và ACD.

Giải:

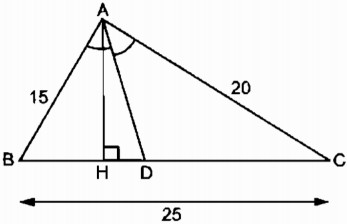
a. Trong tam giác ABC, ta có: AD là đường phân giác của

Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác )

Mà AB = 15(cm); AC = 20 (cm)

Nên \({{DB} \over {DC}} = {{15} \over {20}}\)

Suy ra: \({{DB} \over {DB + DC}} = {{15} \over {15 + 20}}\) (tính chất tỉ lệ thức)

Suy ra: \({{DB} \over {BC}} = {{15} \over {35}}\) \( \Rightarrow DB = {{15} \over {35}}.BC = {{15} \over {35}}.25 = {{75} \over 7}\) (cm)

b. Kẻ AH ⊥ BC

Ta có: \({S_{ABD}} = {1 \over 2}AH.BD;{S_{ADC}} = {1 \over 2}AH.DC\)

Suy ra: \({{{S_{ABD}}} \over {{S_{ADC}}}} = {{{1 \over 2}AH.BD} \over {{1 \over 2}AH.DC}} = {{BD} \over {DC}}\)

Mà \({{DB} \over {DC}} = {{15} \over {20}} = {3 \over 4}\) (chứng minh trên )

Vậy: \({{{S_{ABD}}} \over {{S_{ADC}}}} = {3 \over 4}\)

Câu 18 trang 87 Sách bài tập (SBT) Toán 8 tập 2

Tam giác ABC có các đường phân giác AD, BE và CF

Chứng minh rằng:

\({{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = 1\)

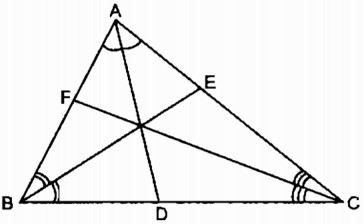
Giải:

Trong tam giác ABC, ta có: AD là đường phân giác của \(\widehat {BAC}\)

Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác ) (1)

BE là đường phân giác \(\widehat {ABC}\)

Suy ra: \({{EC} \over {EA}} = {{BC} \over {AB}}\) (tính chất đường phân giác )        (2)

CF là đường phân giác của \(\widehat {ACB}\)

Suy ra: \({{FA} \over {FB}} = {{CA} \over {CB}}\) (tính chất đường phân giác )       (3)

Nhân từng vế (1), (2) và (3), ta có:

\({{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = {{AB} \over {AC}}.{{BC} \over {AB}}.{{CA} \over {CB}} = 1\)

Câu 19 trang 87 Sách bài tập (SBT) Toán 8 tập 2

Tam giác cân BAC có BA = BC = a, AC = b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N

a. Chứng minh rằng: MN // AC.

b. Tính MN theo a, b

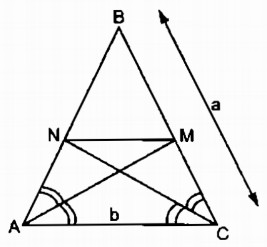
Giải:

a. Trong tam giác BAC, ta có: AM là đường phân giác của \(\widehat {BAC}\)

Suy ra: \({{MC} \over {MB}} = {{AC} \over {AB}}\) (tính chất đường phân giác )     (1)

CN là đường phân giác \(\widehat {BAC}\)

Suy ra: \({{NA} \over {NB}} = {{AC} \over {AB}}\) (tính chất đường phân giác )   (2)

Lại có: AB = CB = a (gt)

Từ (1), (2) và (gt) suy ra: \({{MC} \over {MB}} = {{NA} \over {NB}}\)

Trong tam giác BAC, ta có: \({{NA} \over {NB}} = {{MC} \over {MB}}\)

Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét)

b. Ta có: \({{MC} \over {MB}} = {{AC} \over {AB}}\) (chứng minh trên )

Suy ra: \({{MC + MB} \over {MB}} = {{AC + AB} \over {AB}} \Rightarrow {{CB} \over {MB}} = {{AC + AB} \over {AB}}\)

Hay \({a \over {MC}} = {{b + a} \over a} \Rightarrow MC = {{{a^2}} \over {a + b}}\)

Trong tam giác ABC, ta có:

MN // AC (chứng minh trên )

Và \({{MN} \over {AC}} = {{MB} \over {BC}}\)

Vậy \(MN = {{AC.MB} \over {BC}} = {{b.{{{a^2}} \over {a + b}}} \over a} = {{ab} \over {a + b}}\)

Câu 20 trang 87 Sách bài tập (SBT) Toán 8 tập 2

Tam giác ABC có AB = 12cm, AC = 20cm, BC = 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E thuộc AC)

a. Tính độ dài đoạn thẳng BD, DC và DE

b. Cho biết diện tích tam giác ABC là S, tính diện tích các tam giác ABD, ADE và DCE.

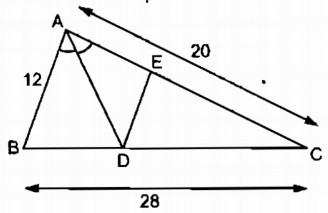
Giải: 

a. Trong tam giác ABC, ta có:

AD là đường phân giác của \(\widehat {BAC}\)

Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\)  (tính chất tia phân giác)

Suy ra: \({{DB} \over {DB + DC}} = {{AB} \over {AB + AC}}\)

Suy ra: \({{DB} \over {BC}} = {{AB} \over {AB + AC}}\)

Suy ra: \(DB = {{BC.AB} \over {AB + AC}} = {{28.12} \over {12 + 20}} = {{21} \over 2} = 10,5\) (cm)

Vậy DC = BC – DB = 28 – 10,5 = 17,5 (cm)

Trong tam giác ABC, ta có: DE // AB

Suy ra: \({{DC} \over {DB}} = {{DE} \over {AB}}\) (Hệ quả định lí Ta-lét )

Vậy: \(DE = {{DC.AB} \over {BC}} = {{17,5.12} \over {28}} = 7,5\)  (cm0

b. Vì ∆ABD và ∆ABC có chung đường cao kẻ từ đỉnh A nên:

\({{{S_{ABD}}} \over {{S_{ABC}}}} = {{DB} \over {BC}} = {{{{21} \over 2}} \over {28}} = {{21} \over {56}} = {3 \over 8}\)

Vậy : \({S_{ABD}} = {3 \over 8}S\)

\({S_{ADC}} = {S_{ABC}} - {S_{ABD}} = S - {3 \over 8}S = {8 \over 8}S - {3 \over 8}S = {5 \over 8}S\)

Vì DE // AB và AD là đường phân giác góc A nên AE = DE.

Ta có: \({{{S_{ADE}}} \over {{S_{ADC}}}} = {{AE} \over {AC}} = {{DE} \over {AC}} = {{7,5} \over {20}}\)

Vậy: \({S_{ADE}} = {{7,5} \over {20}}.{S_{ADC}} = {{7,5} \over {20}}.{5 \over 8}S = {{7,5} \over {32}}S\)

Ta có: \({S_{DCE}} = {S_{ADC}} - {S_{ADE}} = {5 \over 8}S - {{7,5} \over {32}}S = {{12,5} \over {32}}S\).