Câu 10 trang 84 Sách bài tập (SBT) Toán 8 tập 2

Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q (h.9)

Chứng minh rằng MN = PQ.

Giải:

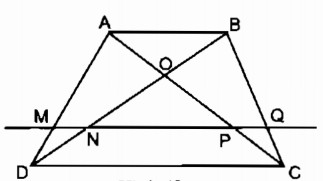
Trong tam giác ADB, ta có: MN // AB (gt)

Suy ra: \({{DN} \over {DB}} = {{MN} \over {AB}}\) (Hệ quả định lí Ta-lét )   (1)

Trong tam giác ACB, ta có: PQ // AB (gt)

Suy ra: \({{CQ} \over {CB}} = {{PQ} \over {AB}}\) (Hệ quả định lí Ta-lét )  (2)

Lại có: NQ // AB (gt)

AB // CD (gt)

Suy ra: NQ // CD

Trong tam giác BDC, ta có: NQ // CD (chứng minh trên)

Suy ra: \({{DN} \over {DB}} = {{CQ} \over {CB}}\)  (Định lí Ta-lét )  (3)

Từ (1), (2) và (3) suy ra: \({{MN} \over {AB}} = {{PQ} \over {AB}}\) hay MN = PQ.

Câu 11 trang 85 Sách bài tập (SBT) Toán 8 tập 2

Cho hình thang ABCD (AB // CD). Trên cạnh bên AD lấy điểm E sao cho \({{AE} \over {ED}} = {p \over q}\) . Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F

Chứng minh rằng: \(EF = {{p.CD + q.AB} \over {p + q}}\)

HD: Kẻ thêm đường chéo AC, cắt EF ở I, rồi áp dụng hệ quả định lí Ta-lét vào các tam giác ADC và CAB.

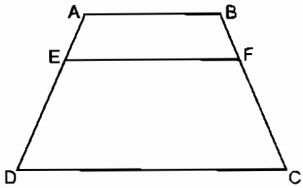
Giải:

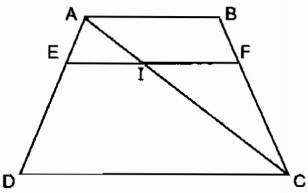
Kẻ đường chéo AC cắt EF tại I.

Trong tam giác AEC, ta có: EI // CD

Suy ra: \({{AE} \over {AD}} = {{EI} \over {CD}}\) (Hệ quả định lí Ta-lét )

Suy ra: \(EI = {{AE} \over {AD}}.CD\)   (1)

Lại có: \({{AE} \over {ED}} = {p \over q}\) (gt)

Suy ra: \({{AE} \over {AE + ED}} = {p \over {p + q}}\)

Suy ra: \({{AE} \over {AD}} = {p \over {p + q}}\)  (2)

Từ (1) và (2) suy ra: \(EI = {p \over {p + d}}.CD\)

Trong tam giác ABC, ta có: IF // AB

Suy ra: \({{BF} \over {FC}} = {{AI} \over {IC}}\) (Định lí Ta-lét )            (3)

Trong tam giác ADC, ta có: EI // CD

Suy ra: \({{AE} \over {ED}} = {{AI} \over {IC}}\) (Định lí Ta-lét )           (4)

Từ (3) và (4) suy ra: \({{BF} \over {FC}} = {{AE} \over {ED}} = {p \over q}\)

Trong tam giác ABC, ta có: IF // BC

Suy ra: \({{IF} \over {AB}} = {{CF} \over {CB}}\) (Hệ quả của định lí Ta-lét)

Suy ra: \(IF = {{CF} \over {CB}}.AB\)           (5)

Ta có: \({{BF} \over {CF}} = {p \over q}\) (cmt)

Suy ra: \({{CF} \over {BF}} = {q \over p} \Rightarrow {{CF} \over {CF + BF}} = {q \over {p + q}} \Rightarrow {{CF} \over {CB}} = {q \over {p + q}}\)   (6)

Từ (5) và (6) suy ra: \(IF = {q \over {p + q}}.AB\)

Vậy: \(EF = EI + {\rm I}F = {p \over {p + q}}.CD + {q \over {p + d}}.AB = {{p.CD + q.AB} \over {p + q}}\)

Câu 12 trang 85 Sách bài tập (SBT) Toán 8 tập 2

Hình thang cân ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O (h.11). Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm.

a. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.

b. So sánh độ dài đoạn thẳng MN với nửa hiệu các độ dài của CD và AB.

Giải:

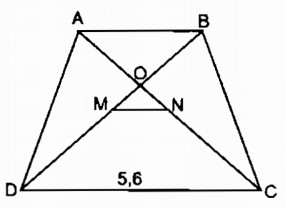
a. Vì ABCD là hình thang cân có AB // CD nên:

AC = BD         (1)

Xét ∆ADC và ∆BCD, ta có:

AC = BD (chứng minh trên )

AD = BC (ABCD cân)

CD cạnh chung

Suy ra: ∆ADC = ∆BCD (c.c.c)

Suy ra: \(\widehat {ACD} = \widehat {BDC}\)

Hay \(\widehat {OCD} = \widehat {ODC}\)

Suy ra tam giác OCD cân tại O

Suy ra:  (tính chất tam giác cân)   (2)

Từ (1) và (2) suy ra: OA = OB

Lại có: MD = 3MO (gt) ⇒ NC = 3NO

Trong tam giác OCD, ta có: \({{MO} \over {MD}} = {{NO} \over {NC}} = {1 \over 3}\)

Suy ra: MN // CD (Định lí đảo của định lí Ta-lét )

Ta có: OD = OM + MD = OM + 3OM = 4OM

Trong tam giác OCD, ta có: MN // CD

Suy ra: \({{OM} \over {OD}} = {{MN} \over {CD}}\)  (Hệ quả định lí Ta-lét )

Suy ra: \({{MN} \over {CD}} = {{OM} \over {4OM}} = {1 \over 4}\)

Suy ra: \(MN = {1 \over 4}CD = {1 \over 4}.5,6 = 1,4\) (cm)

Ta có: MB = MD (gt)

Suy ra: MB = 3OM hay OB = 2OM

Lại có: AB // CD (gt), suy ra: MN // AB

Trong tam giác OAB, ta có: MN // AB

Suy ra: \({{OM} \over {OB}} = {{MN} \over {AB}}\) (Hệ quả định lí Ta-lét )

Suy ra: \({{MN} \over {AB}} = {{OM} \over {2OM}} = {1 \over 2}\)

Vậy AB = 2MN = 2.1,4 = 2,8 (cm)

b. Ta có: \({{CD - AB} \over 2} = {{5,6 - 2,8} \over 2} = {{2,8} \over 2} = 1,4\) (cm)

Vậy MN\( = {{CD - AB} \over 2}\)

Câu 13 trang 85 Sách bài tập (SBT) Toán 8 tập 2

Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm của các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng:

a.  MN// AB;

b. \(MN = {{CD - AB} \over 2}\)

Giải:

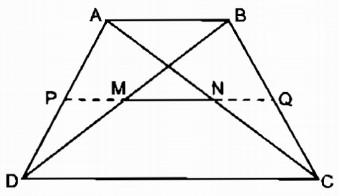
a. Gọi P là trung điểm của AD, nối PM.

Trong tam giác DAB, ta có:

\({{PA} \over {AD}} = {1 \over 2};{{BM} \over {BD}} = {1 \over 2}\)

Suy ra: \({{PA} \over {AD}} = {{BM} \over {BD}}\)

Suy ra: PM // AB (Định lí đảo của định lí Ta-lét)                       (1)

Trong tam giác ACD, ta có: \({{AP} \over {AD}} = {1 \over 2};{{AN} \over {AC}} = {1 \over 2}\)

Suy ra: \({{AP} \over {AD}} = {{AN} \over {AC}}\)

Suy ra: PN // CD ( Định lí đảo định lí Ta-lét)                             (2)

Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.

Vậy MN // CD hay MN // AB.

b. Vì PM là đường trung bình của tam giác DAB nên:

\(PM = {{AB} \over 2}\) (tính chất đường trung bình tam giác)

Vì PN là đường trung bình của tam giác ADC nên:

\(PN = {{AB} \over 2}\) (tính chất đường trung bình tam giác)

Mà PN = PM + MN

Suy ra: MN = PN – PM = \({{CD} \over 2} - {{AB} \over 2} = {{CD - AB} \over 2}\)

Giaibaitap.me