Câu 21 trang 82 Sách bài tập (SBT) Toán 8 tập 1

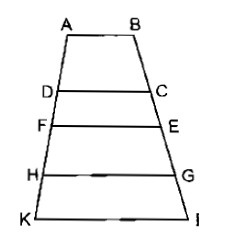
Trên hình 3 có bao nhiêu hình thang ?

Giải:

Trên hình vẽ có tất cả 10 hình thang: ABCD, ABEF, ABGH, ABIK, DCEF, DCGH, DCIK, FEGH, FEIK, HGIK.

Bài 2.1 trang 82 Sách bài tập (SBT) Toán 8 lớp tập 1

Hình thang ABCD (BC// AD) có . Khẳng định nào dưới đây là đúng ?

A. \(\widehat A = {45^0}\)

B. \(\widehat B = {45^0}\)

C. \(\widehat D = {45^0}\)

D. \(\widehat D = {60^0}\)

Giải:

Chọn C. \(\widehat D = {45^0}\)

Câu 2.2 trang 82 Sách bài tập (SBT) Toán lớp 8 tập 1

Hình thang ABCD (AB // CD) có \(\widehat A - \widehat D = {40^0},\widehat A = 2\widehat C\). Tính các góc của hình thang

Giải:

Hình thang ABCD có AB // CD

\( \Rightarrow \widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\eqalign{
& \widehat A - \widehat D = {40^0}(gt) \cr
& \Rightarrow 2\widehat A = {220^0} \Rightarrow \widehat A = {110^0} \cr
& \widehat D = \widehat A - {40^0} = {110^0} - {40^0} = {70^0} \cr
& \widehat A = 2\widehat C(gt) \cr
& \Rightarrow \widehat C = {{\widehat A} \over 2} = {110^0}:2 = {55^0} \cr} \)

\(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)

\( \Rightarrow \widehat B = {180^0} - \widehat C = {180^0} - {55^0} = {125^0}\)

Câu 2.3 trang 82 Sách bài tập (SBT) Toán lớp 8 tập 1

Cho tam giác ABC vuông cân tại A, BC= 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E.

a. Chứng minh rằng AECB là hình thang vuông

b. Tính các góc và các cạnh của hình thang AECB

Giải:

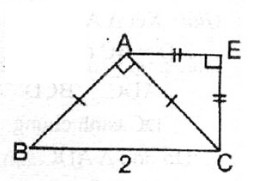
a. ∆ ABC vuông cân tại A

\(\Rightarrow \widehat {ACB} = {45^0}\)

∆ EAC vuông cân tại E

\( \Rightarrow \widehat {EAC} = {45^0}\) 

Suy ra: \(\widehat {EAC} = \widehat {ACB}\)

⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

nên tứ giác AECB là hình thang có \(\widehat E = {90^0}\). Vậy AECB là hình thang vuông

 b) \(\widehat E = \widehat {ECB} = {90^0},\widehat B = {45^0}\)

\(\widehat B + \widehat {EAB} = {180^0}\) (hai góc trong cùng phía bù nhau)

\( \Rightarrow \widehat {EAB} = {180^0} - \widehat B = {180^0} - {45^0} = {135^0}\)

∆ ABC vuông tại A. Theo định lí Py-ta-go ta có:

\(A{B^2} + A{C^2} = B{C^2}\)  mà AB= AC (gt)

\(\eqalign{
& \Rightarrow 2A{B^2} = B{C^2} = {2^2} = 4 \cr
& A{B^2} = 2 \Rightarrow AB = \sqrt 2 (cm) \Rightarrow AC = \sqrt 2 (cm) \cr} \) 

∆ AEC vuông tại E. Theo định lí Py-ta-go ta có:

\(E{A^2} + E{C^2} = A{C^2}\), mà EA = EC (gt)

\(\eqalign{
& \Rightarrow 2E{A^2} = A{C^2} = 2 \cr
& E{A^2} = 1 \cr
& \Rightarrow EA = 1(cm) \Rightarrow EC = 1(cm) \cr} \)

Giaibaitap.me