Câu 30 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.

a. Tứ giác BDEC là hình gì ? Vì sao ?

b. Các điểm D, E ở vị trí nào thì BD = DE = EC ?

Giải:

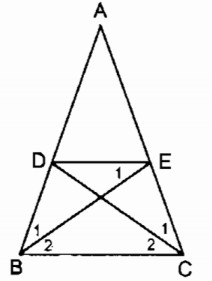
a. AD = AE (gt)

⇒ ∆ ADE cân tại A

\( \Rightarrow \widehat {ADE} = {{{{180}^0} - \widehat A} \over 2}\) 

∆ ABC cân tại A

\( \Rightarrow \widehat {ABC} = {{{{180}^0} - \widehat A} \over 2}\) 

Suy ra:  \(\widehat {ADE} = \widehat {ABC}\)

⇒ DE // BC (vì có cặp góc đồng vị bằng nhau)

Tứ giác BDEC là hình thang

\(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)

Hay \(\widehat {DBC} = \widehat {ECB}\). Vậy BDEC là hình thang cân

b. Ta có: BD = DE ⇒ ∆ BDE cân tại D

\( \Rightarrow {\widehat B_1} = {\widehat E_1}\)

Mà \({\widehat E_1} = {\widehat B_2}\) (so le trong)

\( \Rightarrow {\widehat B_1} = {\widehat B_2}\)

DE = EC ⇒∆ DEC cân tại E

\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)

\({\widehat D_1} = {\widehat C_2}\) (so le trong)

\( \Rightarrow {\widehat C_1} = {\widehat C_2}\)

Vậy khi BE là tia phân giác của \(\widehat {ABC}\), CD là tia phân giác của \(\widehat {ACB}\) thì BD = DE = EC.

Câu 31 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.

Giải:

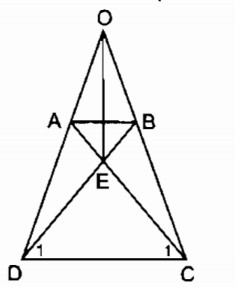
\(\eqalign{
& \widehat {ADC} = \widehat {BCD}\,\,\,\,(gt) \cr 
& \Rightarrow \widehat {ODC} = \widehat {OCD} \cr} \) 

⇒ ∆ OCD cân tại O

⇒ OC = OD

⇒ OA + AD = OB + BC

Mà AD = BC (tính chất hình thang cân)

⇒ OA = OB

Xét ∆ ADC và ∆ BCD :

AD = BC (chứng minh trên)

AC = BD (tính chất hình thang cân)

CD cạnh chung

Do đó: ∆ ADC = ∆ BCD (c.c.c)

\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)

⇒ ∆ EDC cân tại E

⇒ EC = ED nên E thuộc đường trung trực của CD

OC = OD nên O thuộc đường trung trực của CD

E≢ O. Vậy OE là đường trung trực của CD.

BD = AC (chứng minh trên)

⇒ EB + ED = EA + EC mà ED = EC

⇒ EB = EA nên E thuộc đường trung trực AB

E≢ O. Vậy OE là đường trung trực của AB.

Câu 32 trang 83 Sách bài tập (SBT) Toán 8 tập 1

a. Hình thang cân ABCD có đáy nhỏ AB = b, đáy lớn CD = a, đường cao AH.

Chứng minh rằng  (a và b có cùng đơn vị đo)

b. Tính đường cao của hình thang cân có hai đáy 10cm, 26cm và cạnh bên 17cm

Giải:

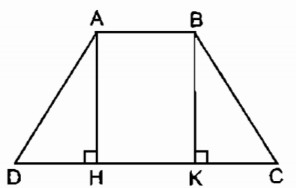
a. Kẻ đường cao BK

Xét hai tam giác vuông AHD và BKC, ta có:

\(\widehat {AHB} = \widehat {BKC} = {90^0}\) 

AD = BC (tính chất hình thang cân)

\(\widehat D = \widehat C\)  (gt)

Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)

⇒ HD = KC

Hình thang ABKH có hai cạnh bên song song nên AB = HK

a−b = DC – AB = DC – HK = HD + KC = 2HD

\( \Rightarrow HD = {{a - b} \over 2}\)

\(HD = DC-HD = a - {{a - b} \over 2} = {{a + b} \over 2}\)

 b. \(HD = {{CD - AB} \over 2} = {{26 - 10} \over 2} = 8\left( {cm} \right)\)

Trong tam giác vuông AHD có \(\widehat {AHD} = {90^0}\)

\(A{D^2} = A{H^2} + H{D^2}\) (định lí Pi-ta-go)

\(\eqalign{
& \Rightarrow A{H^2} = A{D^2} - H{D^2} \cr 
& A{H^2} = {17^2} - {8^2} = 289 - 64 = 225 \cr 
& AH = 15(cm) \cr} \)

Câu 33 trang 83 Sách bài tập (SBT) Toán 8 tập 1

Hình thang cân ABCD có đường chéo DB vuông góc với cạnh bên BC, BD là tia phân giác của góc D. Tính chu vi của hình thang, biết BC = 3cm.

Giải:

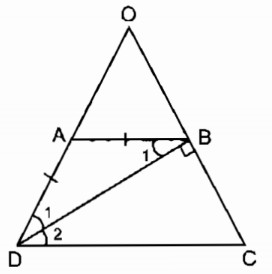
Ta có: AD = BC = 3 (cm)  (tính chất hình thang cân)

\(\widehat {ABD} = \widehat {BDC}\) (so le trong)

\(\eqalign{
& \widehat {ADB} = \widehat {BDC}(gt) \cr 
& \Rightarrow \widehat {ABD} = \widehat {ADB} \cr} \)

⇒ ∆ ABD cân tại A

⇒ AB = AD = 3 (cm)

∆ BDC vuông tại B

\( \Rightarrow \widehat {BDC} + \widehat C = {90^0}\)

\(\widehat {ADC} = \widehat C\) (gt)

Mà \(\widehat {BDC} = {1 \over 2}\widehat {ADC}\) nên  \(\widehat {BDC} = {1 \over 2}\widehat C\)

\(\widehat C + {1 \over 2}\widehat C = {90^0} \Rightarrow \widehat C = {60^0}\)

Từ B kẻ đường thẳng song song AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

\(\widehat {BEC} = \widehat {ADC}\)  (đồng vị )

Suy ra:  \(\widehat {BEC} = \widehat C\)

⇒ ∆ BEC cân tại B có \(\widehat C = {60^0}\)

⇒ ∆ BEC đều

⇒ EC = BC = 3 (cm)

CD = CE + ED = 3 + 3 = 6 (cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3+3 +6 +3=15 (cm)

Giaibaitap.me