Câu 1 trang 82 Sách bài tập (SBT) Toán 8 tập 2

Viết tỉ số của các cặp đoạn thẳng sau:

a. AB = 125cm, CD = 625 cm;

b. EF = 45cm, E’F’ = 13,5dm

c. MN = 555cm, M’N’ = 999cm

d. PQ = 10101cm, P’Q’ = 303,03m

Giải:

a. Ta có:

${{AB} \over {CD}} = {{125} \over {625}} = {1 \over 5}$

b. Đổi: E’F’ = 13,5dm = 135 cm

Ta có:

${{EF} \over {E'F'}} = {{45} \over {135}} = {1 \over 3}$

c. Ta có:

${{MN} \over {M'N'}} = {{555} \over {999}} = {{111.5} \over {111.9}} = {5 \over 9}$

d. Đổi: P’Q’ = 303,03m = 30303cm

Ta có:

${{PQ} \over {P'Q'}} = {{10101} \over {30303}} = {{10101} \over {10101.3}} = {1 \over 3}$

Câu 2 trang 82 Sách bài tập (SBT) Toán 8 tập 2

Đoạn thẳng AB gấp năm lần đoạn thẳng CD; đoạn thẳng A’B’ gấp bảy lần đoạn thẳng CD.

a. Tính tỉ số của hai đoạn thẳng AB và A’B’

b. Cho biết đoạn thẳng MN = 505cm và đoạn thẳng M’N’ = 707cm, hỏi hai đoạn thẳng AB , A’B’ có tỉ lệ với hai đoạn thẳng MN và M’N’ hay không ?

Giải:

a. Chọn đoạn thẳng CD làm đơn vị

Suy ra đoạn thẳng AB = 5 (đơn vị), đoạn thẳng A’B’ = 7 (đơn vị).

Vậy: ${{AB} \over {A'B'}} = {5 \over 7}$

b. Ta có:

${{MN} \over {M'N'}} = {{505} \over {707}} = {{101.5} \over {101.7}} = {5 \over 7}$

Vì ${{AB} \over {A'B'}} = {{MN} \over {M'N'}}$ nên AB và A’B’ tỉ lệ với MN và M’N’.

Câu 3 trang 82 Sách bài tập (SBT) Toán 8 tập 2

Tính độ dài x của các đoạn thẳng trong hình 1, biết rằng các số trên hình cùng đơn vị đo là cm.

Giải:

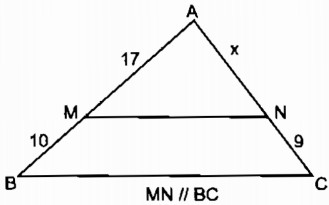
a. Xem hình 1

Trong ∆ ABC, ta có: MN // BC

Suy ra: ${{AM} \over {MB}} = {{AN} \over {NC}}$ (định lí Ta –lét)

Hay ${{17} \over {10}} = {x \over 9}$

Vậy $x = {{17.9} \over {10}} = 15,3$ (cm)

b. Xem hình 2

 Trong ∆ PQR, ta có: EF // QR

Suy ra: ${{EP} \over {PQ}} = {{PF} \over {PR}}$

Hay ${{16} \over x} = {{20} \over {PR}}$

Mà $PR = PF + FR = 20 + 15 = 35$

Vậy $x = {{16.35} \over {20}} = 28$ (cm)

Câu 4 trang 83 Sách bài tập (SBT) Toán 8 tập 2

Cho hình thang ABCD có AB // CD và AB < CD

Đường thẳng song song với đáy AB cắt các cạnh bên CD, BC theo thứ tự tại M và N.

Chứng minh rằng:

a. ${{MA} \over {AD}} = {{NB} \over {BC}}$

b. ${{MA} \over {MD}} = {{NB} \over {NC}}$

c. ${{MD} \over {DA}} = {{NC} \over {CB}}$

HD: Kéo dài các tia DA, CB cắt nhau tại E(h.3), áp dụng định lí Ta-lét trong tam giác và tính chất của tỉ lệ thức để chứng minh.

Giải:

(xem hình 3)

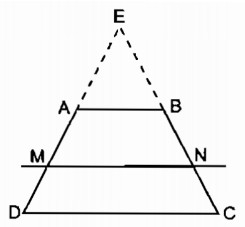
a. Gọi E là giao điểm của AD và BC.

Trong ∆ EMN, ta có: AB // MN (gt)

Suy ra: ${{EA} \over {MA}} = {{EB} \over {NB}}$ (định lí Ta-lét)

Hay ${{EA} \over {EB}} = {{MA} \over {NB}}$  (1)

Trong ∆ EDC, ta có: AB // CD (gt)

Suy ra: ${{EA} \over {AD}} = {{EB} \over {BC}}$ (định lí Ta-lét)

Hay ${{EA} \over {EB}} = {{AD} \over {BC}}$ (2)

Từ (1) và (2) suy ra: ${{MA} \over {NB}} = {{AD} \over {BC}} \Rightarrow {{MA} \over {AD}} = {{NB} \over {BC}}$

b. Ta có: ${{MA} \over {AD}} = {{NB} \over {BC}}$ (gt)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

${{MA} \over {AD - MA}} = {{NB} \over {BC - NB}} \Rightarrow {{MA} \over {MD}} = {{NB} \over {NC}}$

c. Ta có: ${{MA} \over {MD}} = {{NB} \over {NC}}$ (gt)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

${{MA} \over {MD}} = {{NB} \over {NC}} \Rightarrow {{MD} \over {MA + MD}} = {{NC} \over {NB + NC}} \Rightarrow {{MD} \over {DA}} = {{NC} \over {CB}}$

Giaibaitap.me