Bài 2.5 trang 50 sách bài tập (SBT) – Hình học 12.

Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó.

Hướng dẫn làm bài:

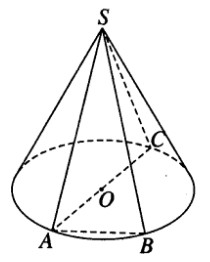
Xét hai đường sinh SA , SB tùy ý của hình nón. Vẽ đường kính AC của đường tròn đáy. Ta có góc ASC là góc ở đỉnh của hình nón. Hai tam giác ASC và ASB có hai cặp cạnh bằng nhau vì chúng cùng là đường sinh của hình nón.

Ta có cạnh \(AC \ge AB\)  nên \(\widehat {{\rm{AS}}C} \ge \widehat {ASB}\) . Đó là điều cần chứng minh.

Bài 2.6 trang 50 sách bài tập (SBT) – Hình học 12.

Cho khối nón có bán kính đáy r = 12 cm và có góc ở đỉnh là \(\alpha  = {120^0}\). Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau.

Hướng dẫn làm bài:

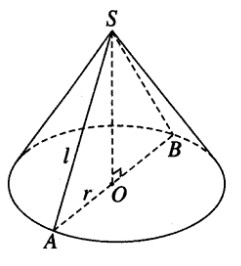
Theo giả thiết ta có góc ở đỉnh của hình nón là \(\widehat {ASB} = \alpha  = {120^0}\). Gọi O là tâm của đường tròn đáy. Ta có: \(\widehat {ASO} = {60^0}\)  và \(\sin {60^0} = {{OA} \over {SA}} = {r \over l}\)   với l là độ dài đường sinh của hình nón.

Vậy \(l = {r \over {\sin {{60}^0}}} = {{12} \over {{{\sqrt 3 } \over 2}}} = {{24} \over {\sqrt 3 }}\)

Khi có hai đường sinh vuông góc với nhau ta có tam giác vuông có diện tích là \({1 \over 2}{l^2}\).  Do đó, diện tích của thiết diện là: \(S = {1 \over 2}{l^2} = {1 \over 2}.{{{{24}^2}} \over 3} = 96(c{m^2})\).

Bài 2.7 trang 50 sách bài tập (SBT) – Hình học 12.

Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A. Một điểm M chạy trên mặt phẳng  (P) sao cho góc \(\widehat {ABM} = \widehat {BMH}\) . Chứng minh rằng  điểm M luôn luôn nằm trên một mặt trụ xoay có trục là AB.

Hướng dẫn làm bài:

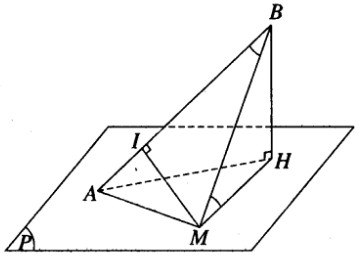
Giải sử ta có điểm M thuộc mặt phẳng (P) thỏa mãn các điều kiện của giả thiết đã cho. Gọi I là hình chiếu vuông góc của M trên AB. Hai tam giác vuông BIM và MHB bằng nhau vì có cạnh huyền chung và một cặp góc nhọn bằng nhau. Do đó  MI = BH không đổi. Vậy điểm M luôn luôn nằm trên mặt trụ trục AB và có bán kính bằng BH.

Bài 2.8 trang 50 sách bài tập (SBT) – Hình học 12.

Cho mặt trụ xoay \((\Im )\)  và một điểm S cố định nằm ngoài \((\Im )\)  . Một đường thẳng d thay đổi luôn luôn đi qua S cắt \((\Im )\)  tại A và B. Chứng minh rằng trung điểm I của đoạn thẳng AB luôn luôn nằm trên một mặt trụ xác định.

Hướng dẫn làm bài:

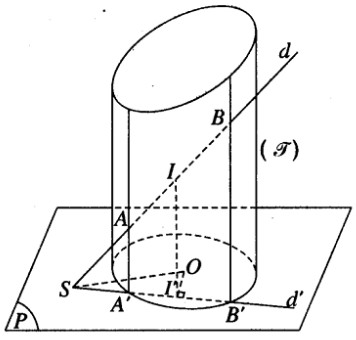
Gọi (P) là mặt phẳng đi qua S và vuông góc với trục của mặt trụ \((\Im )\). Mặt phẳng (P) cắt \((\Im )\)  theo một đường tròn tâm O. Ta hãy xét một vị trí của đường thẳng d. Gọi A, B là giao điểm của d với \((\Im )\)   và I là trung điểm của đoạn AB. Chiếu A, B, I theo phương vuông góc với mặt phẳng (P) ta được các điểm theo thứ tự là A’ , B’ , I’ thẳng hàng với S, trong đó A’, B’ nằm trên đường tròn tâm O trong mặt phẳng (P) và I’ là trung điểm  của đoạn A’B’. Do đó điểm I’ luôn luôn nằm trên đường tròn đường kính SO trong mặt phẳng (P) và đường thẳng II’ vuông góc với (P). Ta suy ra đường thẳng II’ nằm trên mặt trụ \((\Im ')\)  chứa đường tròn đường kính SO nằm trong (P) và có trục song song với trục của mặt trụ \((\Im )\)  .

Tất nhiên, điểm I chỉ nằm trong phần mặt trụ \((\Im ')\) thuộc miền trong của mặt trụ \((\Im )\) 

Giaibaitap.me