Bài 6 trang 133 sgk toán 8 tập 2
Cho tam giác ABC và đường trung tuyến BM. Trên đoạn thẳng BM lấy điểm D sao cho . Tia AD cắt BC ở K. Tìm tỉ số diện tích của tam giác ABK và tam giác ABC.
Hướng dẫn làm bài:
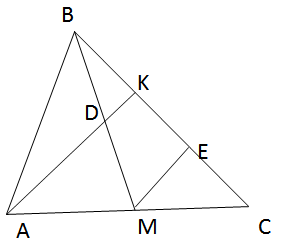
Kẻ ME song song với AK (E ∈ BC).
Ta có: \({{BK} \over {KE}} = {{BD} \over {DM}} = {1 \over 2} = > KE = 2BK\)
ME là đường trung bình của tam giác ACK nên EC = KE = 2BK
Ta có : BC = BK + KE + EC = 5BK => \({{BK} \over {BC}} = {1 \over 5}\)
\({{{s_{ABK}}} \over {{S_{ABC}}}} = {{BK} \over {BC}} = {1 \over 5}\) (hai tam giác ABK và ABC có chung đường cao hạ từ A).
Bài 7 trang 133 sgk toán 8 tập 2
Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE.
Hướng dẫn làm bài:
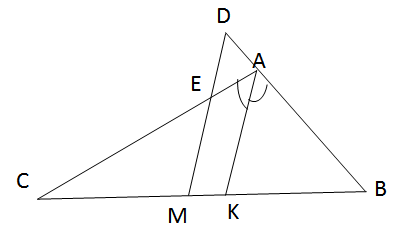
AK là đường phân giác của tam giác ABC nên
\({{KB} \over {AB}} = {{KC} \over {AC}}\) (1)
Vì MD // AK nên:
∆ABK ∽ ∆DBM và ∆ECM ∽ ∆ACK
Do đó:
\({{KB} \over {AB}} = {{BM} \over {BD}}\) và \( {{CM} \over {CE}} = {{KC} \over {AC}}\) (2)
Từ (1) và (2) ta có: \({{BM} \over {BD}} = {{CM} \over {CE}}\) (3)
Do BM = CM (giả thiết) nên từ (3) suy ra : BD = CE
Bài 8 trang 133 sgk toán 8 tập 2
Trên hình 151 cho thấy ta có thể xác định chiều rộng BB’ của khúc song bằng cách xét hai tam giác đồng dạng ABC và AB’C’. Hãy tính BB’ nếu AC = 100 m, AC’ = 32 m, AB’ = 34m.
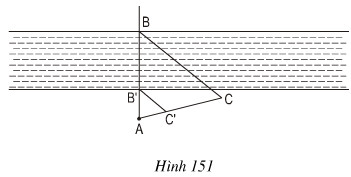
Hướng dẫn làm bài:
Ta có: \({{AB} \over {AB'}} = {{AC} \over {AC'}} = > {{AB' + BB'} \over {AB'}} = {{AC} \over {AC'}}\)
=> \({{34 + BB'} \over {34}} = {{100} \over {32}} = > BB' = 72,25\left( m \right)\)
Bài 9 trang 133 sgk toán 8 tập 2
Cho tam giác ABC có AB < AC, D là một điểm nằm giữa A và C. Chứng minh rằng : \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)
Hướng dẫn làm bài:
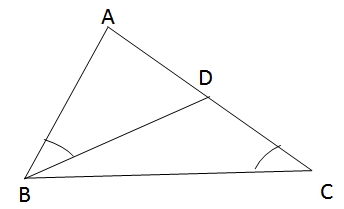
a) Chứng minh \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)
∆ABD ∽ ∆ACB (g.g) => \({{AB} \over {AC}} = {{AD} \over {AB}} = > A{B^2} = AC.AD\)
b) Chứng minh \(A{B^2} = AC.AD = > \widehat {ABD} = \widehat {ACB}\)
\(A{B^2} = AC.AD = > {{AB} \over {AC}} = {{AD} \over {AB}}\)
Góc A chung nên ∆ABD ∽ ∆ACB (c.g.c)
=> \(\widehat {ABD} = \widehat {ACB}\)
Vậy \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)
Bài 10 trang 133 sgk toán 8 tập 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 12 cm, AD = 16 cm, AA’ = 25 cm.
a)Chứng minh các tứ giác ACC’A’, BDD’B’ là những hình chữ nhật.
b)Chứng minh rằng AC’2 = AB2 + AD2 + AA’2.
c)Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
Hướng dẫn làm bài:
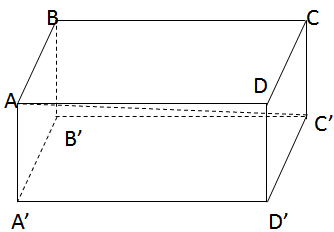
a) Chứng minh rằng mỗi mặt chéo là một hình bình hành có một góc vuông.
b) Trong tam giác vuông ACC’:
AC’2 = AC2 + CC’2 = AC2 + AA’2
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh: \({S_{xq}} = 2ph = 2\left( {AB + AD} \right).AA'\)
=2(12 + 16)25 = 1400 (cm2)
Diện tích một đáy: Sd = AB . AD = 12. 16 = 192 (cm2)
Diện tích toàn phần: Stp = Sxq + 2Sd = 1400 + 2.192 = 1784 (cm2)
Thể tích: V= abc = AB.AD.AA’ = 12. 16. 25 = 4800 (cm2)
Bài 11 trang 133 sgk toán 8 tập 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20 cm, cạnh bên SA = 24cm.
a)Tính chiều cao SO rồi tính thể tích của hình chóp.
b)Tính diện tích toàn phần của hình chóp.
Hướng dẫn làm bài:
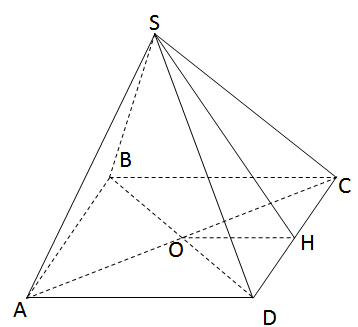
a) \(S{O^2} = S{D^2} - O{D^2} = {24^2} - {\left( {{{20\sqrt 2 } \over 2}} \right)^2} = 376\)
= > \(SO \approx 19,4\left( {cm} \right)\)
\(V = {1 \over 3}{.20^2}.19,4 \approx 2586,6\) (cm2)
b)Gọi H là trung điểm của CD.
\(S{H^2} = S{D^2} - D{H^2} = {24^2} - {\left( {{{20} \over 2}} \right)^2} = 476\)
=>SH ≈ 21,8 (cm)
\({S_{xq}} \approx {1 \over 2}.80.21,8 \approx 872\) (cm2)
\({S_d} = A{B^2} = {20^2} = 400\left( {c{m^2}} \right)\)
Nên \({S_{tp}} = {S_{xq}} + {S_d} = 872 + 2.400 = 1672{\left( {cm} \right)^2}\)
Giaibaitap.me
