Câu 58 trang 149 Sách bài tập (SBT) Toán 8 tập 2
Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước cho ở hình 145.
(xem hình 145)
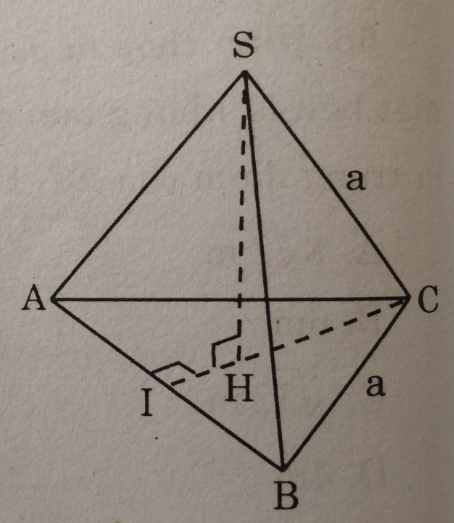
Giải:
Hình vẽ đã cho là hình chóp có ba mặt xung quanh và mặt đáy là các tam giác đều bằng nhau có cạnh là a. Áp dụng định lí Pi-ta-go vào tam giác vuông CIA, ta có:
Suy ra: \(C{I^2} = A{C^2} - A{I^2} = {a^2} - {\left( {{a \over 2}} \right)^2} = {{3{a^2}} \over 4}\)
Vậy CI = \({{a\sqrt 3 } \over 2}\)
Ta có: \({S_{ABC}} = {1 \over 2}.a.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 4}\) (đvdt)
Vậy \({S_{TP}} = 4.{{{a^2}\sqrt 3 } \over 4} = {a^2}\sqrt 3 \) (đvdt)
Câu 59 trang 150 Sách bài tập (SBT) Toán 8 tập 2
Cho hình chóp tứ giác đều (h.146). Xem hình và điền số thích hợp vào các ô còn trống ở bảng sau:
(hình 146 trang 150 sbt)
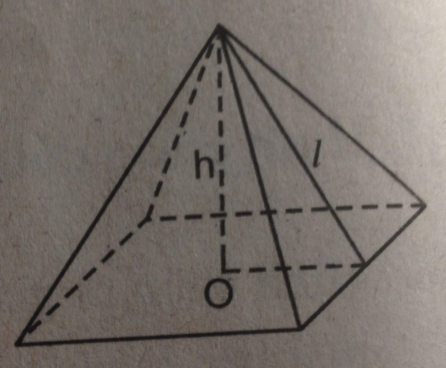
|
Chiều cao (h) |
8 |
15 |
|
|
|
Trung đoạn l |
10 |
|
15 |
|
|
Cạnh đáy |
|
16 |
12 |
10 |
|
Sxq |
|
|
|
120 |
Giải:
|
Chiều cao (h) |
8 |
15 |
\(\sqrt {189} \) |
\(\sqrt {11} \) |
|
Trung đoạn l |
10 |
17 |
15 |
6 |
|
Cạnh đáy |
12 |
16 |
12 |
10 |
|
Sxq |
240 |
544 |
360 |
120 |
Câu 60 trang 150 Sách bài tập (SBT) Toán 8 tập 2
Một hình chóp tứ giác đều có độ dài cạnh đáy là 6cm, chiều cao là 4cm thì diện tích xung quanh là:
A. 128cm2
B. 96cm2
C. 120cm2
D. 60cm2
E. 84cm2
Hãy chọn kết quả đúng.
Giải:
Kẻ trung đoạn của hình chóp.
Áp dụng định lí Pi-ta-go ta tính được trung đoạn của hình chóp bằng 5cm.
Diện tích xung quanh của hình chóp là: \({S_{xq}} = 4.{1 \over 2}.6.5 = 60(c{m^2})\)
Vậy chọn đáp án D.
Câu 61 trang 150 Sách bài tập (SBT) Toán 8 tập 2
Hình chóp đều S.ABC có cạnh đáy a = 12cm, chiều cao h = 8cm. Hãy tính diện tích xung quanh của hình chóp đó.
Giải:
(hình trang 155 sgbt)
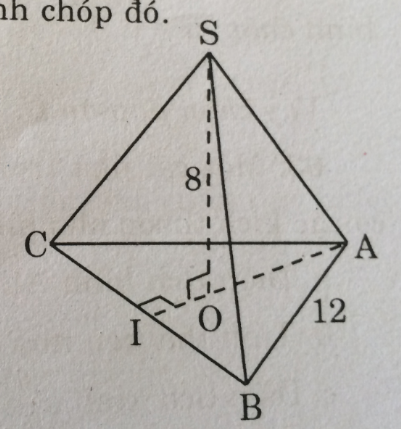
Kẻ AO kéo dài cắt BC tại I.
Ta có: AI ⊥ BC (tính chất tam giác đều)
BI = IC = \({1 \over 2}BC\)
Áp dụng định lí Pi-ta-go vào tam giác vuông AIB, ta có: $A{B^2} = B{I^2} + A{I^2}$
Suy ra:
\(\eqalign{ & A{I^2} = A{B^2} - B{I^2} = {12^2} - {6^2} = 108 \cr & AI = \sqrt {108} (cm) \cr} \)
Vì tam giác ABC đều nên O là trọng tâm của tam giác ABC.
Ta có: \(OI = {1 \over 3}AI = {1 \over 3}\sqrt {108} \) (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông SOI, ta có:
\(\eqalign{ & S{I^2} = S{O^2} + O{I^2} = {8^2} + {1 \over 9}.108 = 76 \cr & SI = \sqrt {76} (cm) \cr} \)
Vậy \({S_{xq}} = Pd = \left[ {\left( {12.3} \right):2} \right].\sqrt {76} = 18\sqrt {76} (c{m^2})\)
Giaibaitap.me
Giải bài tập trang 150, 151 bài thể tích hình chóp đều Sách bài tập (SBT) Toán 8 tập 2. Câu 62: Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình 147 dưới đây...
Giải bài tập trang 152 bài thể tích hình chóp đều Sách bài tập (SBT) Toán 8 tập 2. Câu 66: Thể tích hình chóp đều cho theo các kích thước ở hình 150 là...
Giải bài tập trang 153, 154 bài ôn tập chương IV - Hình lăng trụ đứng hình chóp đều Sách bài tập (SBT) Toán 8 tập 2. Câu 73: Xét hình lập phương...
Giải bài tập trang 153 bài thể tích hình chóp đều Sách bài tập (SBT) Toán 8 tập 2. Câu 70: Tính thể tích và diện tích toàn phần các hình chóp đều dưới đây...
