Câu 44 trang 85 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC, đường trung tuyến AM. Gọi O là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB và AC. Gọi AA’, BB’, CC’ là các đường vuông góc kẻ từ A, B, C đến đường thẳng d. Chứng minh rằng:

\({\rm{AA' = }}{{BB' + CC'} \over 2}\)

Giải:

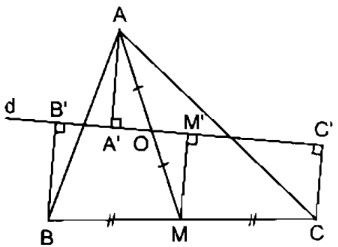
Ta có: BB’ ⊥ d (gt)

            CC’ ⊥ d (gt)

Suy ra: BB’ // CC’

Tứ giác BB’CC’ là hình thang

Kẻ MM’ ⊥ d

 ⇒ MM’ // BB’ // CC’

Nên MM’ là đường trung bình của hình thang BB’CC’

\( \Rightarrow MM' = {{BB' + CC'} \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

Xét hai tam giác vuông AA’O và MM’O:

\(\widehat {OA'A} = \widehat {OM'M}\)

AO = MO (gt)

\(\widehat {AOA'} = \widehat {MOM'}\) (đối đỉnh)

Do đó: ∆ AA’O = ∆ MM’O (cạnh huyền, góc nhọn)

⇒ AA’ = MM’ (2)

Từ (1) và (2) suy ra: \({\rm{AA' = }}{{BB' + CC'} \over 2}\).

Câu 4.1 trang 85 Sách bài tập (SBT) Toán lớp 8 tập 1

Trên hình bs.1, ta có AB // CD // EF // GH và AC = CE = EG. Biết CD = 9, GH = 13. Các độ dài AB và EF bằng:

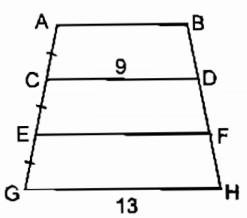
A. 8 và 10                                                B.6 và 12

C. 7 và 11                                                D. 7 và 12

Giải:

Chọn C. 7 và 11.

Câu 4.2 trang 85 Sách bài tập (SBT) Toán lớp 8 tập 1

Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm. Gọi C là trung điểm của AB. Tính khoảng cách từ C đến đường thẳng d.

Giải:

a) Trường hợp A và B nằm trên một nửa mặt phẳng bờ chứa đường thẳng d.

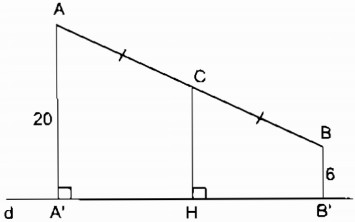
Gọi A’, B’ là chân đường vuông góc kẻ từ A và B đến d

AA’ ⊥ d; BB’ ⊥ d ⇒ AA’ // BB’

Tứ giác ABB’A’ là hình thang. Kẻ CH ⊥ d

⇒ CH // AA’ // BB’ nên CG là đường trung bình của hình thang ABB’A’

\( \Rightarrow CH = {{AA' + BB'} \over 2} = {{20 + 6} \over 2} = 13\,\,\left( {cm} \right)\)

b) Trường hợp A và B nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng d

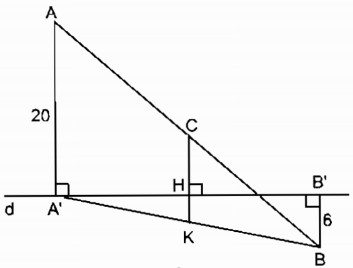
Kẻ CH ⊥ d cắt A’B tại K

⇒ CH // AA’ // BB’

Trong ∆ AA’B ta có: AC = CB

Mà CK // AA’ nên A’K = KB và CK là đường trung bình của tam giác AA’B

\( \Rightarrow CK = {{AA'} \over 2}\)  (tính chất đường trung bình của tam giác)

\(CK = {{20} \over 2} = 10\,\,\left( {cm} \right)\)

Trong ∆ A’BB’ có A’K = KB và KH // BB’

Nên KH là đường trung bình của ∆ A’BB’

\( \Rightarrow KH = {{BB'} \over 2}\) (tính chất đường trung bình của tam giác)

\( \Rightarrow KH = {6 \over 2} = 3\,\,\left( {cm} \right)\)

CH = CK – KH = 10 – 3 = 7(cm)

Câu 4.3 trang 85 Sách bài tập (SBT) Toán lớp 8 tập 1

Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Gọi K là giao điểm của DM và AC. Chứng minh rằng AK = 2KC.

Giải:

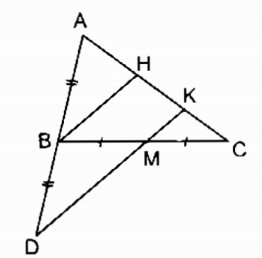
Gọi H là trung điểm của AK

Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.

⇒ BH // DK (tính chất đường trung bình của tam giác)

Hay BH // MK

Trong ∆ BCH ta có M là trung điểm của BC

MK // BH

⇒ CK = HK

AK = AH + HK = 2HK

Suy ra: AH = 2 CK.

Giaibaitap.me