Câu 45 trang 85 Sách bài tập (SBT) Toán 8 tập 1
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 5cm và \(\widehat B = {35^0}\).
Giải:
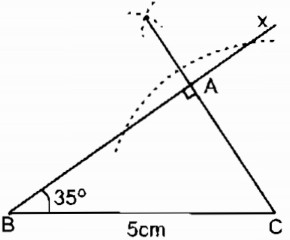
Cách dựng:
- Dựng đoạn BC = 5cm
- Dựng góc \(\widehat {CBx} = {35^0}\)
- Dựng CA ⊥ Bx ta có ∆ ABC dựng được.
Chứng minh: ∆ ABC có \(\widehat A = {90^0},\widehat B = {35^0}\), BC = 5cm. Thỏa mãn điều kiện bài toán.
Câu 46 trang 85 Sách bài tập (SBT) Toán 8 tập 1
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm.
Giải:
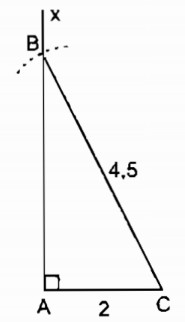
Cách dựng:
- Dựng đoạn AC = 2cm
- Dựng góc \(\widehat {CAx} = {90^0}\)
- Dựng cung tròn tâm C bán kính 4,5cm cắt Ax tại B. Nối CB ta có ∆ ABC cần dựng
Chứng minh: ∆ ABC có \(\widehat A = {90^0}\), AC = 2cm, BC = 4,5cm. Thỏa mãn điều kiện bài toán.
Câu 47 trang 85 Sách bài tập (SBT) Toán 8 tập 1
Dựng góc \({30^0}\) bằng thước và compa.
Giải:
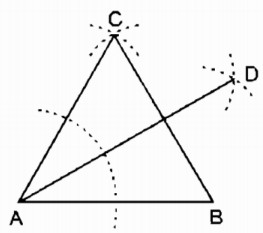
Cách dựng:
- Dựng tam giác đều ABC
- Dựng tia phân giác AD của \(\widehat {BAC}\) ta có \(\widehat {BAD} = {30^0}\)
Chứng minh: ∆ ABC đều
\( \Rightarrow \widehat {BAC} = {60^0}\)
\(\widehat {BAD} = {{\widehat {BAC}} \over 2}\) (tính chất tia phân giác)
\( \Rightarrow \widehat {BAD} = {30^0}\)
Câu 48 trang 85 Sách bài tập (SBT) Toán 8 tập 1
Dựng hình thang cân ABCD (AB // CD), biết CD = 3cm, AC = 4cm, \(\widehat D = {70^0}\).
Giải:
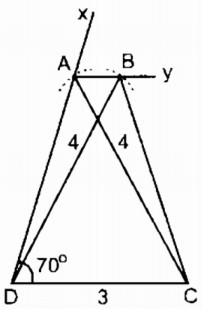
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiên bài toán, ta thấy ∆ACD xác định được vì biết CD = 3cm, \(\widehat D = {70^0}\), AC = 4cm.
Ta cần xác định đỉnh B. Đỉnh B thỏa mãn hai điều kiện:
- Nằm trên tia Ay // CD
- B cách D một khoảng bằng 4 cm
Cách dựng:
- Dựng đoạn CD = 3cm
- Dựng góc \(\widehat {CDx} = {70^0}\)
- Trên nửa mặt phẳng bờ CD chứa tia Dx dựng cung tròn tâm C bán kính 4cm cắt Dx tại A.
- Dựng tia Ay // CD
- Trên nửa mặt phẳng bờ CD chứa điểm A, dựng cung tròn tâm D bán kính 4cm cắt Ay tại B
- Nối BC ta có hình thang ABCD cần dựng.
Chứng minh: Thật vậy theo cách dựng ta có AB // CD nên tứ giác ABCD là hình thang có CD = 3cm, \(\widehat {ADC} = {70^0}\), AC = BD = 4cm.
Vậy ABCD là hình thang cân.
Biện luận: ∆ ACD luôn dựng được nên hình thang ABCD luôn dựng được.
Bài toán có một nghiệm hình.
Giaibaitap.me
Giải bài tập trang 86 bài 5 dựng hình bằng thước và com pa. Dựng hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 49: Dựng hình thang ABCD (AB // CD), biết ...
Giải bài tập trang 86 bài 5 dựng hình bằng thước và com pa. Dựng hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 5.1: Dựng hình thang cân ABCD(AB // CD) biết BC = 3cm, AC = 2cm, đường cao bằng 2,5cm...
Giải bài tập trang 86, 87 bài 6 đối xứng trục Sách bài tập (SBT) Toán 8 tập 1. Câu 60: Chứng minh rằng AD = AE...
Giải bài tập trang 86 bài 5 dựng hình bằng thước và com pa. Dựng hình thang Sách bài tập (SBT) Toán 8 tập 1. Câu 53: Dựng hình thang cân ABCD(AB // CD), biết AD = 2cm, CD = 4cm, AC = 3,5cm...
