Bài 41 trang 132 sgk toán 8 tập 1

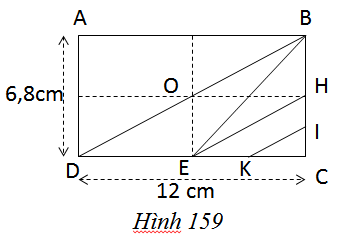
Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HD, DC, EC (h.159)

Tính : a)Diện tích tam giác DBE ;

b)Diện tích tứ giác EHIK.

Hướng dẫn làm bài:

a)Ta có:   \(DE = {1 \over 2}DC( = {1 \over 2}.12 = 6\left( {cm} \right)\)

Nên   \({S_{DBE}} = {1 \over 2}.DE.BC = {1 \over 2}.6.6,8 = 20,4\left( {c{m^3}} \right)\)

b)Ta có :  \(HC = {1 \over 2}BC = {1 \over 2}.6,8 = 3,4\left( {cm} \right)\)

 \(HI = {1 \over 2}HC = {1 \over 2}.3,4 = 1,7\left( {cm} \right)\)

EC = DE = 6cm                                                

 \(EK = KC = {1 \over 2}EC = {1 \over 2}.6 = 3\left( {cm} \right)\)

Do đó  \({S_{EHIK}} = {S_{EHK}} + {S_{HKI}} = {1 \over 2}EK.HC + {1 \over 2}HI.KC\)

= \({1 \over 2}EK.HC + {1 \over 2}EK.HI = {1 \over 2}EK\left( {HC + HI} \right)\)

 \({S_{EHIK}} = {1 \over 2}.3.\left( {3,4 + 1,7} \right) = {1 \over 2}.3.5,1 = 7,65(c{m^2})\)

Cách khác:

 \({S_{EHIK}} = {S_{EHC}} - {S_{KIC}} = {1 \over 2}EC.HC - {1 \over 2}KC.IC\)

= \({1 \over 2}.6.3,4 - {1 \over 2}.3.1,7\)

= \(10,2 - 2,55 = 7,65\left( {c{m^2}} \right)\)

Bài 42 trang 132 sgk toán 8 tập 1

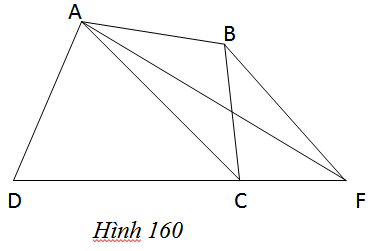
Trên hình 160 (AC//BF), hãy tìm tam giác có diện tích bằng diện tích của tứ giác ABCD.

Hướng dẫn làm bài:

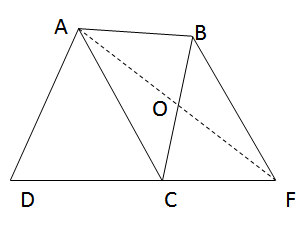
Nối AF ta được tam giấc ADF có diện tích bằng diện tích tứ giác ABCD. Thật vậy, do AC// BF nên  \({S_{ABC}} = {S_{AFC}}\) vì có cùng đáy AC và cùng chiều cao là khoảng cách giữa hai đường thẳng song song AC, BF. Suy ra \({S_{ABO}} = {S_{CFO}}\).

Do đó  \({S_{ADF}} = {S_{AOCD}} + {S_{CFO}} = {S_{AOCD}} + {S_{ABO}}\)

Vậy  \({S_{ADF}} = {S_{ABCD}}\)

Từ đó ta suy ra cách vẽ tam giác có diện tích bằng diện tích của tứ giác ABCD cho trước:

Vẽ đường chéo AC. Từ B vẽ BF // AC (F nằm trên đường thẳng DC). Nối AF. Ta được tam giác ADF là tam giác có diện tích bằng diện tích của tứ giác ABCD.

Bài 43 trang 132 sgk toán 8 tập 1

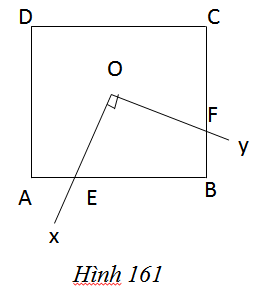
Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F (h.161)

Tính diện tích tứ giác OEBF.

Hướng dẫn làm bài:

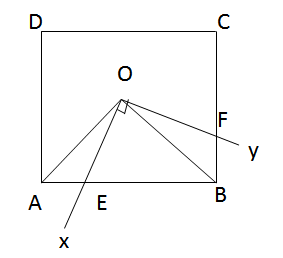
Nối OA, OB. Hai tam giác AOE và BOF có:

 \(\widehat {AOE} = \widehat {BOF}\) (cùng phụ với BOE)

OA = OB (O là tâm đối xứng)

 \(\widehat {OAE} = \widehat {OBF} = {45^0}\)

Nên ∆AOE = ∆BOF

Do đó  \({S_{OEBF}} = {S_{OEB}} + {S_{OBF}} \)

\(= {S_{OEB}} + {S_{OAE}} = {S_{OAE}} + {S_{OEB}} = {S_{OAB}}\)

Vậy  \({S_{OEBF}} = {1 \over 4}{S_{ABCD}}\)

Bài 44 trang 133 sgk toán 8 tập 1

Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.

Hướng dẫn làm bài:

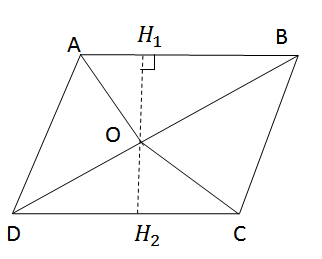
Từ O lẻ đường thẳng d vuông góc với AB ở H₁, cắt CD ở H₂.

Ta có OH₁  ⊥ AB

Mà AB // CD

Nên OH₂    ⊥ CD

Do đó  \({S_{ABO}} + {S_{CDO}} = {1 \over 2}O{H_1}.AB + {1 \over 2}O{H_2}.CD\)

= \({1 \over 2}AB\left( {O{H_1} + O{H_2}} \right)\)

= \({1 \over 2}.AB.{H_1}.{H_2}\)

Nên   \({S_{ABO}} + {S_{CDO}} = {1 \over 2}{S_{ABCD}}\) ( 1)

Tương tự  \({S_{BCO}} + {S_{DAO}} = {1 \over 2}{S_{ABCD}}\) (2)

Từ (1) và (2) suy ra :

 \({S_{ABO}} + {S_{CDO}} = {S_{BCO}} + {S_{DAO}}\)

Bài 45 trang 133 sgk toán 8 tập 1

Hai cạnh của một hình bình hành có độ dài là 6 cm và 4 cm. Một trong các đường cao có độ dài là 5 cm. Tính độ dài đường cao kia.

Hướng dẫn làm bài:                                                               

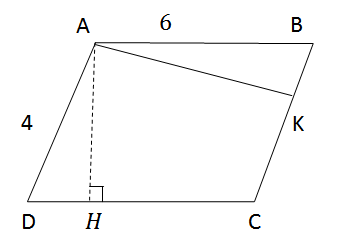
Cho hình bình hành ABCD. Gọi AH, AK lần lượt là đường cao kẻ từ A đến CD, BC.

Ta có:  \({S_{ABCD}} = AB.AH = AD.AK\)

 \({S_{ABCD}} = 6.AH = 4.AK\)

Một đường cao có độ dài 5 cm thì đó là AK vì AK < AB (5 <6), không thể là AH vì AH < 4.

Vậy  \(6.AH = 4.5 = 20 =  > AH = {{10} \over 3}\left( {cm} \right)\)

Bài 46 trang 133 sgk toán 8 tập 1

Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng  diện tích của tam giác ABC.

Hướng dẫn làm bài:                                

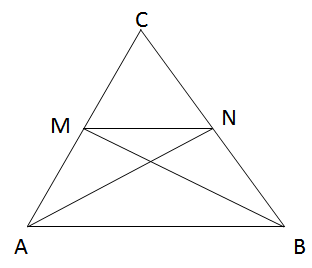
Vẽ hai trung tuyến AN, BM của ∆ABC. Ta có:

 \({S_{ABN}} = {1 \over 2}{S_{ABC}}\)

(có cùng đường cao từ đỉnh A, đáy  \(BN = {1 \over 2}BC)\)

 \({S_{AMN}} = {S_{MNC}}\) (có cùn đường cao từ đỉnh N, đáy AM = MC).

Suy ra  \({S_{AMN}} = {S_{MNC}} = {1 \over 2}{S_{ANC}} = {1 \over 4}{S_{ABC}}\)

Vậy  \({S_{ABN}} + {S_{AMN}} = {1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} = {3 \over 4}{S_{ABC}}\)

Tức là  \({S_{ABMN}} = {3 \over 4}{S_{ABC}}\)

Bài 47 trang 133 sgk toán 8 tập 1

Vẽ ba đường trung tuyến của một tam giác (h.162). Chứng minh sáu tam giác: 1, 2, 3, 4, 5, 6 có diện tích bằng nhau.

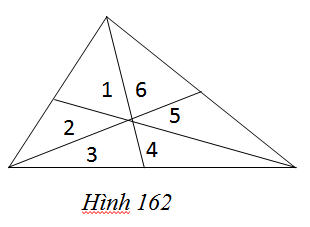
Hướng dẫn làm bài:

Theo tính chất của trung tuyến, suy ra:

 \({S_1} = {S_2}\) (có đáy bằng nhau và cùng chiều cao) (1)

 \({S_3} = {S_4}\) (có đáy bằng nhau và cùng chiều cao) (2)

 \({S_5} = {S_6}\)(có đáy bằng nhau và cùng chiều cao) (3)

Lại có:  \({S_1} + {S_2} + {S_3} + {S_4} + {S_5} + {S_6}\left( { = {1 \over 2}{S_{ABC}}} \right)\) (4)

Kết hợp (4) với (1), (2), (3) suy ra  \({S_1} = {S_6}\) (4’)

Và  \({S_1} + {S_2} + {S_6} = {S_3} + {S_4} + {S_{5}}\left( { = {1 \over 2}{S_{ABC}}} \right)\) (5)

Kết hợp (5) với  (1), (2), (3) suy ra  \({S_2} = {S_3}\) (5’)

Và \({S_1} + {S_6} + {S_5} = {S_2} + {S_3} + {S_{4}}\left( { = {1 \over 2}{S_{ABC}}} \right)\) (6)

Kết hợp (6) với (1), (2), (3) suy ra  \({S_4} = {S_5}\) (6’)

Từ (4’),  (5’), (6’) và kết hợp với  (1), (2), (3) ta có :

 \({S_1} = {S_2} = {S_3} = {S_4} = {S_5} = {S_6}\)

Giaibaitap.me