Bài 16 trang 75 sgk toán 8 tập 1

Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài giải:  

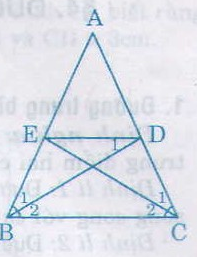
a)  ∆ABD và  ∆ACE có

AB = AC (gt)

\(\widehat{A}\) chung

\(\widehat{B_{1}}\) = \(\widehat{C_{1}}\) \(\left ( =\frac{1}{2}\widehat{B}=\frac{1}{2}\widehat{C} \right )\)

Nên ∆ABD = ∆ACE (g.c.g)

Suy ra AD = AE

Chứng minh BEDC là hình thang cân như câu a của bài 15.

b) Vì BEDC là hình thang cân nên DE // BC.

Suy ra \(\widehat{_{D_{1}}}\) = \(\widehat{B_{2}}\) (so le trong)

Lại có \(\widehat{B_{2}}\) = \(\widehat{B_{1}}\) nên \(\widehat{B_{1}}\) = \(\widehat{_{D_{1}}}\)

Do đó tam giác EBD cân. Suy ra EB = ED.

Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài 17 trang 75 sgk toán 8 tập 1

 Hình thang ABCD (AB // CD) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng ABCD là hình thang cân.

Bài giải:

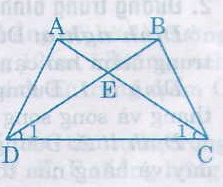
Gọi E là giao điểm của AC và BD.

∆ECD có \(\widehat{C_{1}}=\widehat{D}\) (do \(\widehat{ACD}=\widehat{BDC}\)) nên là tam giác cân.

Suy ra EC = ED        (1)

Tương tự EA = EB      (2)

Từ (1) và (2) suy ra AC = BD

Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.

Bài 18 trang 75 sgk toán 8 tập 1

Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.

Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:

a) ∆BDE là tam giác cân.

b) ∆ACD = ∆BDC.

c) Hình thang ABCD là hình thang cân.

Bài giải:

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:

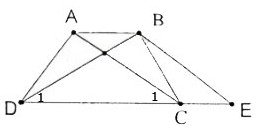
             AC = BE   (1)     

Theo giả thiết AC = BD    (2)

Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.

b) Ta có AC // BE suy ra 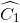 =  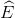     (3)

  ∆BDE cân tại B (câu a) nên 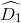 =  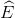     (4)

Từ (3) và (4) suy ra  =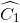 

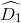
Xét  ∆ACD và  ∆BCD có AC = BD (gt)

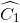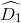                =  (cmt)

CD cạnh chung

Nên ∆ACD = ∆BDC (c.g.c)

c) ∆ACD = ∆BDC (câu b)

Suy ra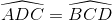 

Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

Bài 19 trang 75 sgk toán 8 tập 1

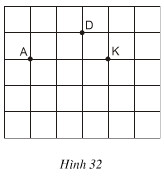
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân

.

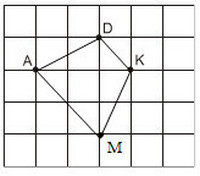
Bài giải: 

Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM₁ (với AK là đáy) và hình thang ADKM₂ (với DK là đáy).

Giaibaitap.me