Câu 118 trang 94 Sách bài tập (SBT) Toán 8 tập 1

Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.

Giải:                                                                         

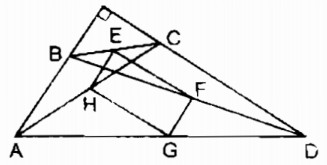
Trong ∆ BCD ta có:

E là trung điểm của BC (gt)

F là trung điểm của BD (gt)

nên EF là đường trung bình của ∆ BCD

⇒ EF // CD và EF= \({1 \over 2}\)CD (1)

Trong ∆ ACD ta có:

H là trung điểm của AC (gt)

G là trung điểm của AD (gt)

nên HG là đường trung bình của ∆ ACD

⇒ HG // AC và HG = \({1 \over 2}\)AC (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Mặt khác: EF // CD (chứng minh trên)

                   AB ⊥ CD(gt)

Suy ra EF ⊥ AB

Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB

Suy ra: HE ⊥ EF hay \(\widehat {FEH} = {90^0}\)

Vậy hình bình hành EFGH là hình chữ nhật.

Câu 119 trang 94 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.

Giải:                                                                       

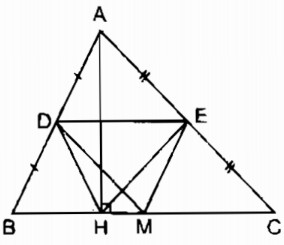
Vì D là trung điểm của AB (gt)

E là trung điểm của AC (gt)

nên DE là đường trung bình của tam giác ABC

⇒ DE // BC hay DE = HM

Suy ra: Tứ giác DEMH là hình thang

M là trung điểm của BC (gt)

nên DM là đường trung bình của ∆ BAC

⇒ DM = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) (1)

Trong tam giác vuông AHC có\(\widehat {AHC} = {90^0}\).

 HE là đường trung tuyến thuộc cạnh huyền AC.

⇒ HE = \({1 \over 2}\)AC (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: DM = HE

Vậy hình thang DEMH là hình thang cân (vì có hai đường chéo bằng nhau)

Câu 120 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.

Giải:                                                                      

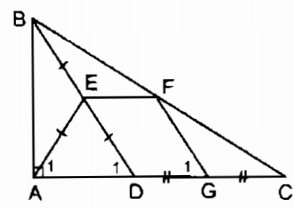
Trong ∆ BDC ta có:

E là trung điểm của BD (gt)

F là trung điểm của BC (gt)

nên EF là đường trung bình của ∆ BDC

⇒ EF // DC

hay EF // AG

Suy ra: Tứ giác AEFG là hình thang

G là trung điểm của DC (gt)

nên FG là đường trung bình của ∆ CBD

⇒ FG // BD ⇒ \({\widehat G_1} = {\widehat D_1}\) (đồng vị) (1)

Trong tam giác ABD vuông tại A có AE là trung tuyến thuộc cạnh huyền BD

⇒ AE = ED = \({1 \over 2}\)BD (tính chất tam giác vuông)

nên ∆ AED cân tại E \( \Rightarrow {\widehat A_1} = {\widehat D_1}\)  (2)

Từ (1) và (2) suy ra: \({\widehat A_1} = {\widehat G_1}\)

Vậy hình thang AEFG là hình thang cân (theo định nghĩa).

Giaibaitap.me