Câu 128 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào ?

Giải:                                                               

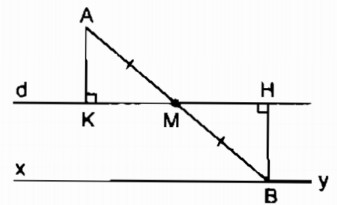
Kẻ  AK ⊥ d, BH ⊥ d

M thay đổi trên d, B đối xứng với A qua M nên AM = MB

Xét hai tam giác vuông AKM và BHM:

\(\widehat {AKM} = \widehat {BHM} = {90^0}\)

AM = MB (chứng minh trên)

\(\widehat {AMK} = \widehat {BMH}\) (đối đỉnh)

Do đó: ∆ AKM = ∆ BHM (cạnh huyền, góc nhọn) ⇒ AK = BH

Điểm A cố định, đường thẳng d cố định nên AK không thay đổi

M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không đổi nên B chuyển động trên đường thẳng xy song song với d một khoảng bằng AK.

Câu 129 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ?

Giải:                                                              

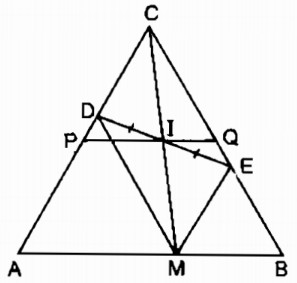
Gọi giao điểm của AD và BE là C.

∆ ABC có: \(\widehat A = {60^0}\) (vì ∆ ADM đều)

                  \(\widehat B = {60^0}\) (vì ∆ BEM đều)

Suy ra: ∆ ABC đều, AC = AB = BC nên điểm C cố định

\(\widehat A = \widehat {EMB} = {60^0}\)

⇒ ME // AC (vì có cặp góc đồng vị bằng nhau)

hay ME // DC

\(\widehat {DMA} = \widehat B = {60^0}\)

⇒ MD // BC (vì có cặp góc đồng vị bằng nhau)

hay MD // EC

Tứ giác CDME là hình bình hành

I là trung điểm của DE nên I là trung điểm của CM

Kẻ CH ⊥ AB, IK ⊥ AB ⇒ IK // CH

Trong ∆ CHM ta có:

CI = IM

IK // CH

nên IK là đường trung bình của ∆ CHM ⇒ IK = \({1 \over 2}\)CH

C cố định ⇒ CH không đổi ⇒ IK =\({1 \over 2}\)CH không thay đổi nên I chuyển động trên đường thẳng song song AB, cách AB một khoảng bằng \({1 \over 2}\)CH.

Khi M trùng với A thì I trùng trung điểm P của AC.

Khi M trùng với B thì I trùng với trung điểm Q của BC.

Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm của AC, Q là trung điểm của BC)

Câu 130 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bởi hai đường chéo.

Giải:                                                                     

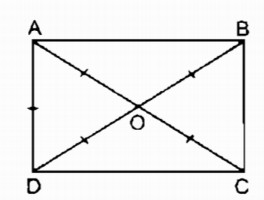
Gọi O là giao điểm của hai đường chéo AC và BD.

AC = BD (tính chất hình chữ nhật)

⇒ OA = OD = \({1 \over 2}\)AC

AD = \({1 \over 2}\)AC (gt)

Suy ra: OA = OD = AD

⇒ ∆ OAD đều

\( \Rightarrow \widehat {AOD} = {60^0}\)

Câu 131 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Dựng hình chữ nhật ABCD, biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng 100°.

Giải:                                                                     

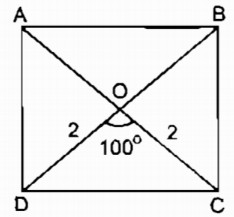
Cách dựng:

       -            Dựng ∆ OAB biết OA = OB = 2cm.
\(\widehat {AOB} = {100^0}\)

       -            Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm

       -            Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm

Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng.

Chứng minh:

OA = OC, OB = OD nên tứ giác ABCD là hình bình hành

AC = BD = 4(cm) nên hình bình hành ABCD là hình chữ nhật

Lại có : \(\widehat {AOB} = {100^0}\)

Giaibaitap.me