Câu 9.1 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Một hình chữ nhật có hai cạnh kề bằng nhau 4cm và 6cm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu xentimét ?
A. 8cm
B. \(\sqrt {52} \)cm
C. 9cm
D. \(\sqrt {42} \)cm
Hãy chọn phương án đúng.
Giải:
Chọn (B) \(\sqrt {52} \) (cm) đúng
Câu 9.2 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.
Giải:
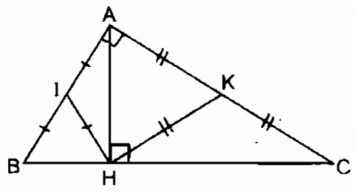
∆ AHB vuông tại H có HI là đường trung tuyến thuộc cạnh huyền AB
⇒ HI = IA = \({1 \over 2}\)AB (tính chất tam giác vuông)
⇒ ∆ IAH cân tại I
\( \Rightarrow \widehat {IAH} = \widehat {IHA}\) (1)
∆ AHC vuông tại H có HK là đường trung tuyến thuộc cạnh huyền AC
⇒ HK = KA = \({1 \over 2}\)AC (tính chất tam giác vuông)
⇒ ∆ KAH cân tại K \( \Rightarrow \widehat {KAH} = \widehat {KHA}\) (2)
\(\widehat {IHK} = \widehat {IHA} + \widehat {KHA}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {IHK} = \widehat {IAH} + \widehat {KAH} = \widehat {IAK} = \widehat {BAC} = {90^0}\).
Câu 9.3 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành.
Giải:
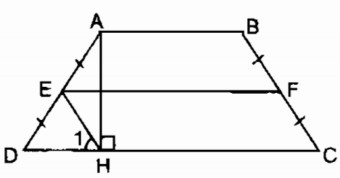
Ta có: E là trung điểm của AD (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của hình thang ABCD
⇒ EF // CD hay EF // CH
∆ AHD vuông tại H có HE là đường trung tuyến thuộc cạnh huyền AD.
Ta có: HE = ED = \({1 \over 2}\)AD (tính chất tam giác vuông)
⇒ ∆ EDH cân tại E
\( \Rightarrow \widehat D = {\widehat H_1}\) (tính chất tam giác cân)
\(\widehat D = \widehat C\) (vì ABCD là hình thang cân)
Suy ra: \({\widehat H_1} = \widehat C\)
⇒ EH // CF (vì có cặp góc đồng vị bằng nhau)
Vậy tứ giác EFCH là hình bình hành.
Giaibaitap.me
Giải bài tập trang 96 bài 10 đường thẳng song song với một đường thẳng cho trước Sách bài tập (SBT) Toán 8 tập 1. Câu 128: Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d...
Giải bài tập trang 96, 97 bài 11 hình thoi Sách bài tập (SBT) Toán 8 tập 1. Câu 132: Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là đỉnh của một hình thoi...
Giải bài tập trang 96 bài 10 đường thẳng song song với một đường thẳng cho trước Sách bài tập (SBT) Toán 8 tập 1. Câu 10.1: Tập hợp giao điểm hai đường chéo của hình chữ nhật ABCD có A và B cố định là...
Giải bài tập trang 96, 97, 98 bài 11 hình thoi Sách bài tập (SBT) Toán 8 tập 1. Câu 136: Cho hình thoi ABCD. Kẻ hai đường cao AH, AK. Chứng minh rằng AH = AK...
