Bài 1 trang 43 SGK Vật Lý 12 Nâng cao

Động năng của vật nặng dao động điều hoà biến đổi theo thời gian

A. Theo một hàm dạng sin.                                         

B. Tuần hoàn với chu kì \(T\).

C. Tuần hoàn với chu kì \({T \over 2}\).                                        

D. Không đổi.

Giải

Động năng của vật nặng dao động điều hoà biến đổi theo thời gian tuần hoàn với chu kì \({T \over 2}\).

Chọn đáp án C.

Bài  2 trang 43 SGK Vật Lý 12 Nâng cao

Một vật có khối lượng \(750\) g dao động điều hoà với biên độ \(4\) cm và chu kì \(T = 2\) s. Tính năng lượng của dao động. 

Giải

Vật dao động điều hoà có \(m = 750\) (g) = \(0,75\) (kg), \(A= 4\) (cm), \(T = 2\) (s).

Năng lượng của dao động : 

\(\eqalign{
& W = {1 \over 2}m{\omega ^2}{A^2} = {1 \over 2}m{\left( {{{2\pi } \over T}} \right)^2}{A^2} \cr
& \Rightarrow W = {1 \over 2}.0,75.{\left( {{{2\pi } \over 2}} \right)^2}.{(0,04)^2} = 0,006(J). \cr} \)

Bài 3 trang 43 SGK Vật Lý 12 Nâng cao

Tính thế năng, động năng và cơ năng của con lắc đơn ở một vị trí bất kì (li độ góc \(\alpha \)) và thử lại rằng cơ năng không đổi trong chuyển động.

Giải

Xét con lắc đơn, ở một vị trí bất kì (có li độ góc \(\alpha \))

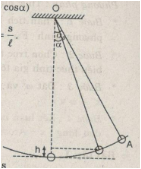
a) Biểu thức thế năng :    \({W_t} = mgh = mg\ell (1 - \cos \alpha )\)

Với dao động nhỏ :\(1 - \cos \alpha = {{{\alpha ^2}} \over 2}\text{ và }\alpha = {s \over \ell }.\)

Thay vào  \( \Rightarrow {W_t} = {1 \over 2}m{g \over \ell }{s^2} = {1 \over 2}m{\omega ^2}{s^2}\)                                                 

b) Biểu thức động năng :\({W_đ} = {1 \over 2}m{v^2}\)

với \({v^2} = 2g\ell (\cos \alpha - \cos {\alpha _0}).\)

Dao động nhỏ :

\(1 - \cos \alpha = {{{\alpha ^2}} \over 2};1 - \cos {\alpha _0} = {{\alpha _0^2} \over 2}\) và \(\alpha = {s \over \ell }.\)

Thay vào :\({W_đ} = {1 \over 2}m{\omega ^2}(s_0^2 - {s^2}).\)

c) Cơ năng :\(W = {W_đ} + {W_t} = {1 \over 2}m{\omega ^2}(s_0^2 - {s^2}) - {1 \over 2}m{\omega ^2}{s^2}\)

\( \Rightarrow {W} = {1 \over 2}m{\omega ^2}s_0^2\)  không đổi trong chuyển động.

Bài 4 trang 43 SGK Vật Lý 12 Nâng cao

Dựa vào định luật bảo toàn cơ năng, tính :

a) Vận tốc của vật nặng trong con lắc lò xo khi đi qua vị trí cân bằng theo biên độ A.

b) Vận tốc của con lắc đơn khi đi qua vị trí cân bằng theo biên độ góc \({\alpha _0}\).

Giải

Dựa vào định luật bảo toàn cơ năng, ta tính được :

a) Vận tốc của vật nặng trong con lắc lò xo khi đi qua vị trí cân bằng :

\(x = 0 \Rightarrow {W_t} = 0\) và \(\eqalign{& W = {W_{{_{đ\max }}}} = {1 \over 2}mv_{\max }^2 \cr & \Rightarrow W = {1 \over 2}m{(v)^2} = {1 \over 2}m{(\omega A)^2} \Rightarrow v = \pm A\omega . \cr} \)

b) Vận tốc con lắc đơn khi đi qua vị trí cân bằng theo biên độ góc \({\alpha _0}\)

\(\alpha = 0 \Rightarrow {W_t} = 0\) và \(\eqalign{& W = {W_đ} \Leftrightarrow {1 \over 2}m{\omega ^2}s_0^2 = {1 \over 2}m{v^2} \cr & \Rightarrow v = \pm \omega {s_0} = \pm \sqrt {2gl(1 - \cos {\alpha _0})} . \cr} \)

Giaibaitap.me