Câu 85 trang 90 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA’, BB’, DD’ là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng ming rằng AA’ = BB’ + DD’.

Giải:                                                        

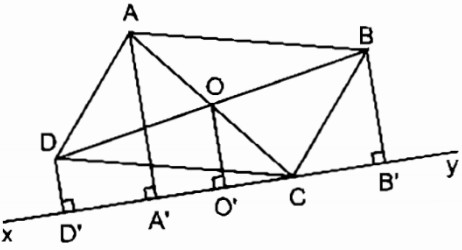
Gọi O là giao điểm của hai đường chéo AC và BD.

Kẻ OO’ ⊥ xy

Ta có: BB’ ⊥ xy (gt)

           DD’ ⊥ xy (gt)

Suy ra: BB’ // OO’ // DD’

Tứ giác BB’D’D là hình thang

OB = OD (tính chất hình bình hành)

nên O’B’ = O’D’ do đó OO’ là đường trung bình của hình thang BB’D’D

⇒ OO’\( = {{BB' + {\rm{DD}}'} \over 2}\) (tính chất đường trung bình hình thang) (1)

AA’ ⊥ xy (gt)

OO’ ⊥ xy (theo cách vẽ)

Suy ra: AA’ // OO’

Trong ∆ ACA’ ta có: OA = OC ( tính chất hình bình hành)

OO’ // AA’ nên OO’ là đường trung bình của ∆ ACA’

⇒ OO’ \( = {1 \over 2}\)AA’ (tính chất đường trung bình của tam giác)

⇒ AA’ = 2OO’ (2)

Từ  (1) và (2) suy ra: AA’ = BB’ + DD’.

Câu 86 trang 90 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi  AA’, BB’, CC’, DD’ là đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA’, BB’, CC’, DD’.

Giải:                                                           

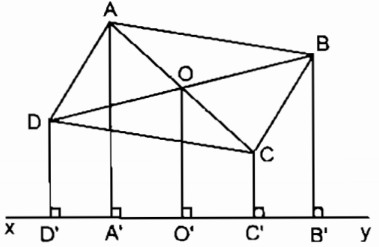
Gọi O là giao điểm của AC và BD

Kẻ OO’ ⊥ xy

      AA’ ⊥ xy (gt)

      CC’ ⊥ xy (gt)                                                                                                                                

Suy ra: AA’// OO’ // CC’

Tứ giác ACCA’ là hình thang có: OA = OC (chứng minh trên)

OO’ // AA’ nên OO’ là đường trung bình của hình thang ACC’A’.

⇒ OO’  \(   = {{{\rm{AA'}} + CC'} \over 2}\) (tính chất đường trung bình của hình thang) (1)

BB’ ⊥ xy (gt)

DD’ ⊥ xy (gt)

OO’ ⊥ xy (theo cách vẽ)

Suy ra: BB’ // OO’ // DD’

Tứ giác BDD’B’ là hình thang có: OB = OD (chứng minh trên)

OO’ // BB’ nên OO’ là đường trung bình của hình thang BDD’B’

⇒ OO’ \( = {{BB' + {\rm{DD}}'} \over 2}\) (tính chất đường trung bình của hình thang) (2)

Từ (1) và (2) suy ra: AA’ + CC’ = BB’ + DD’

Câu 87 trang 90 Sách bài tập (SBT) Toán 8 tập 1

Cho hình bình hành ABCD có\(\widehat A = \alpha  > {90^0}\). Ở phía ngoài hình bình hành, vẽ các tam giác đều ADF, ABE.

a. Tính \(\widehat {EAF}\)

b. Chứng minh rằng tam giác CEF là tam giác đều.

Giải:                                                                     

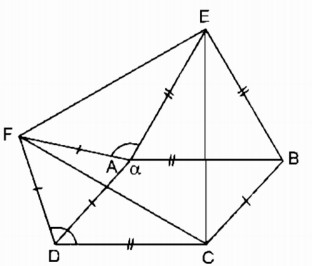
a. Vì \(\eqalign{  & \widehat {BAD} + \widehat {BAE} + \widehat {EAF} + \widehat {FAD} = {360^0}  \cr  &  \Rightarrow \widehat {EAF} = {360^0} - \left( {\widehat {BAD} + \widehat {BAE} + \widehat {FAD}} \right) \cr} \)

mà \(\widehat {BAD} = \alpha \) (gt)

\(\widehat {BAE} = {60^0}\) (∆ BAE đều)

\(\widehat {FAD} = {60^0}\) (∆ FAD đều)

nên \(\widehat {EAF} = {360^0} - \left( {\alpha  + {{60}^0} + {{60}^0}} \right) = {240^0} - \alpha \)

b. Ta có: \(\widehat {ADC} + \widehat {BAD} = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\eqalign{  &  \Rightarrow \widehat {ADC} = {180^0} - \widehat {BAD} = {180^0} - \alpha   \cr  & \widehat {CDF} = \widehat {ADC} + \widehat {ADF} = {180^0} - \alpha  + {60^0} = {240^0} - \alpha  \cr} \)

Suy ra: \(\widehat {CDF} = \widehat {EAF}\)

Xét ∆ AEF và ∆ DCF:

AF = DF (vì ∆ ADF đều)

AE = DC (vì cùng bằng AB)

\(\widehat {CDF} = \widehat {EAF}\) (chứng minh trên)

Do đó ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)

\(\widehat {ADC} = \widehat {ABC}\) (tính chất hình bình hành)

\(\widehat {CBE} = \widehat {ABC} + {60^0} = \widehat {ADC} + {60^0} = {180^0} - \alpha  + {60^0} = {240^0} - \alpha \)

Xét ∆ BCE và ∆ DCF:

BE = CD (vì cùng bằng AB)

\(\widehat {CBE} = \widehat {CDF} = {240^0} - \alpha \)

BC = DF (vì cùng bằng AD)

Do đó: ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)

Từ (1) và (2) suy ra : EF = CF = CE. Vậy ∆ ECF đều.

Giaibaitap.me