Câu 81 trang 90 Sách bài tập (SBT) Toán 8 tập 1

Chu vi hình bình hành ABCD bằng 10cm, chu vi tam giác ABD bằng 9cm. Tính độ dài BD.

Giải:                                                               

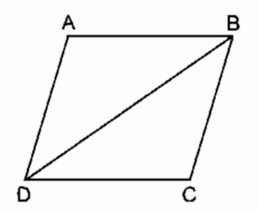
Chu vi hình bình hành ABCD bằng 10cm

nên (AB + AD).2 = 10 (cm)

\(⇒ AB + AD = {{10} \over 2} =5\) (cm)

Chu vi của ∆ ABD bằng :

AB + AD +BD = 9 (cm)

⇒ BD = 9 – ( AB + AD) = 9 – 5 = 4 (cm)

Câu 82 trang 90 Sách bài tập (SBT) Toán 8 tập 1

Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE // CF.

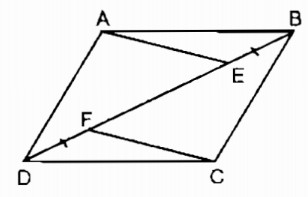
 Giải:                                                                 

 Gọi O là giao điểm của AC và BD, ta có:

 (tính chất hình bình hành)

Xét ∆ AEB và ∆ CFD :

AB = CD (tính chất hình bình hành)

\(\widehat {ABE} = \widehat {CDF}\) (so le trong)

BE = DF (gt)                               

Do đó: ∆ AEB = ∆ CFD (c.g.c)

⇒ BE = DF

Ta có: OB = OE + BE

           OD = OF + DF

Suy ra: OE = OF

Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường) // CF

Câu 83 trang 90 Sách bài tập (SBT) Toán 8 tập 1

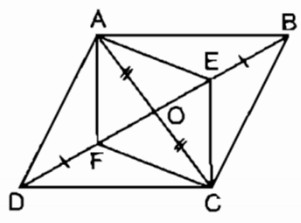
Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng :

a. EMFN là hình bình hành.

b. Các đường thẳng AC, EF, MN đồng quy.

Giải:                                                                    

Xét tứ giác AECF, ta có:

AB // CD (gt)

hay AE // CF

AE \( = {1 \over 2}\)AB (gt)

CF \(= {1 \over 2}\)CD (gt)

AB = CD (tính chất hình bình hành)

Suy ra: AE = CF

Tứ giác AECF là hình bình hành ( vì có một cặp cạnh đối diện song song và bằng nhau) ⇒ AF // CE hay EN // FM (1)

Xét tứ giác BFDE ta có:

AB // CD (gt) hay BE // DF

BE \( = {1 \over 2}\)AB (gt)

DF \( = {1 \over 2}\)CD (gt)

AB = CD ( tính chất hình bình hành)

Suy ra: BE = DF

Tứ giác BFDE là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)

⇒ BF // DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa)

b. Gọi O là giao điểm của AC và EF

Tứ giác AECF là hình bình hành ⇒ OE = OF

Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm mỗi đường.

Suy ra: MN đi qua trung điểm O của EF

Vậy AC, EF, MN đồng quy tại O.

Câu 84 trang 90 Sách bài tập (SBT) Toán 8 tập 1

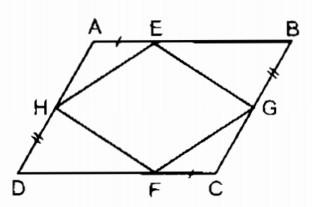
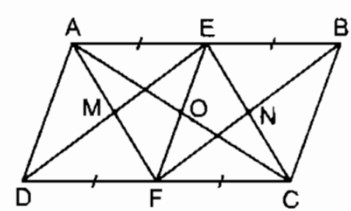
Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:

a. EGFH là hình bình hành

b. Các đường thẳng AC, BD, EF, GH đồng quy.

Giải:                                                                      

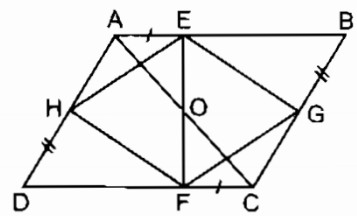
a. Xét ∆ AEH và ∆ CFG:

AE = CF

\(\widehat A = \widehat C\) (tính chất hình bình hành)

AH = CG (vì AD = BC và DH = BG)

Do đó: ∆ AEH = ∆ CFG (c.g.c)

⇒ EH = FG

Xét ∆ BEG và ∆DFH:

DH = BG (gt)

\(\widehat B = \widehat D\) (tính chất hình bình hành)

BE = DF (vì AB = CD và AE = CF)

Do đó: ∆ BEG = ∆DFH (c.g.c)

⇒ EG = FH

Suy ra: Tứ giác EGFH là hình bình hành (vì có cắc cặp cạnh đối bằng nhau)

b. Gọi O là giao điểm của AC và EF.

Xét tứ giác AECF:

AB // CD (gt) hay AE // CF

AE = CF (gt)

Suy ra: Tứ giác AECF là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau)

⇒ O là trung điểm của AC và EF

Tứ giác ABCD là hình bình hành có O là trung điểm của AC nên O cũng là trung điểm của BD.

Tứ giác EGFH là hình bình hành có O là trung điểm của EF nên O cùng là trung điểm của GH.

Vậy AC, BD, GH đồng quy tại O.

Giaibaitap.me