Câu 106 trang 93 Sách bài tập (SBT) Toán 8 tập 1

Tính đường chéo d của một hình chữ nhật, biết độ dài các cạnh a = 3cm, b = 5cm (làm tròn kết quả đến chữ số thập phân thứ nhất).

Giải:

Giả sử hình chữ nhật ABCD có AB = a = 3cm; BC = b = 5cm; BD = d

Trong tam giác vuông ABC theo định lý Py-ta-go ta có:

\(\eqalign{  & {d^2} = {a^2} + {b^2}  \cr  &  \Rightarrow {d^2} = {3^2} + {5^2} = 9 + 25 = 34  \cr  & d = \sqrt {34}  \approx 5,8(cm) \cr} \)

Câu 107 trang 93 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng trong hình chữ nhật:

a. Giao điểm của hai đường chéo là tâm đối xứng của hình.

b. Hai đường thẳng đi qua trung điểm của hai cạnh đối là hai trục đối xứng của hình.

Giải:                                                                 

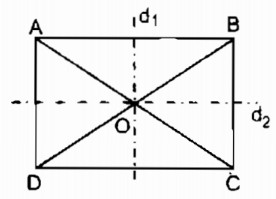
a. Gọi O là giao điểm của hai đường chéo AC và BD.

Vì hình chữ nhật là một hình bình hành nên điểm O là tâm đối xứng của nó.

b. Ta biết trong hình thang cân đường thẳng đi qua trung điểm của hai đáy là trục đối xứng của nó.

Theo định nghĩa ta có hình chữ nhật cũng là một hình thang cân. Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai cạnh đáy AB và CD thì đường thẳng \({d_1}\) đi qua trung điểm của AB và CD là trục đối xứng của hình chữ nhật ABCD.

Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai đáy là AD và BC nên đường thẳng \({d_2}\) đi qua trung điểm của AD và BC là trục đối xứng của hình chữ nhật ABCD.

Câu 108 trang 93 Sách bài tập (SBT) Toán 8 tập 1

Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10cm (làm tròn kết quả đến chữ số thập phân thứ nhất)

Giải:                                                                          

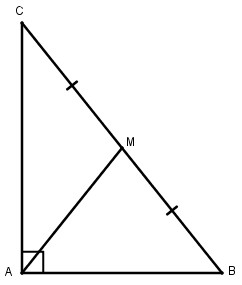
Giả sử ∆ ABC có \(\widehat A = {90^0}\) , M trung điểm của BC; AB = 5cm; AC = 10cm. Theo định lý Pi-ta-go ta có:

\(\eqalign{  & B{C^2} = A{B^2} + A{C^2}  \cr  & BC = \sqrt {{5^2} + {{10}^2}}  = \sqrt {125}  \approx 11,2(cm) \cr} \)

AM \( = {1 \over 2}\) BC (tính chất tam giác vuông)

⇒ AM \( \approx {1 \over 2}.11,2 = 5,6\) (cm)

Câu 109 trang 93 Sách bài tập (SBT) Toán 8 tập 1

Tính x trên hình 16 (đơn vị đo : cm)

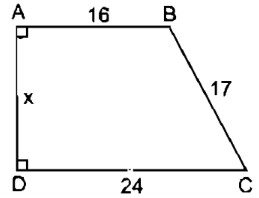
Giải:                                                                           

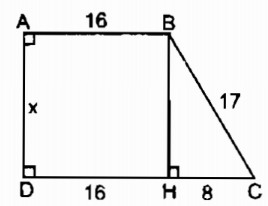
Kẻ BH ⊥ CD

\(\widehat A = {90^0},\widehat D = {90^0},\widehat {BHD} = {90^0}\)

Suy ra: Tứ giác ABHD là hình chữ nhật (vì có ba góc vuông)

⇒ AB = DH, BH = AD

    HC = CD – DH

    CD – AB = 24 – 16 = 8 (cm)

Trong tam giác vuông BHC, theo định lí Pi-ta-go ta có:

\(\eqalign{  & B{C^2} = B{H^2} + H{C^2}  \cr  &  \Rightarrow B{H^2} = B{C^2} - H{C^2}  \cr  & B{H^2} = {17^2} - {8^2} = 289 - 64 = 225  \cr  & BH = \sqrt {225}  = 15(cm)  \cr  & x = AD = BH = 15(cm) \cr} \)

Giaibaitap.me